算法详解 - 自适应辛普森法
前置知识
我们可以看道一个奇怪的式子:
\[ \int^R_L f(x)\, \textrm{d}x \]
究竟是什么意思呢?其实就是求函数 \(f(x)\) 在 \(L\) 到 \(R\) 之间的定值积分。在讲求值之前,要先讲一下映射、函数和积分。
映射
再讲函数之前,先要讲一讲映射。首先我们考虑有两个非空集合 \(X\) 和 \(Y\),如果存在一种法则 \(f\),使得 \(X\) 中的每一个元素 \(x\),按法则 \(f\),在集合 \(Y\) 中有唯一确定的元素 \(y\) 与之对应。那么此时我们称 \(f\) 为 \(X\) 到 \(Y\) 的映射,形式化的记作:
\[ f:X\to Y \]
在这之中,我们把 \(y\) 称为元素 \(x\) 在映射 \(f\) 下的像,记作:
\[ y=f(x) \]
而元素 \(x\) 称为元素 \(y\) 在映射 \(f\) 中的一个原像。
映射有两个必须知道的基本概念,值域和定义域。其中:
- 值域:即映射的所有像组成的集合。
- 定义域:即映射的所有原像组成的集合。
对于辛普森法,关于映射,这些就已经足够了,想了解更多,可以去翻看一下《高等数学第7版-上册》。
函数
或许接触过函数的人看到映射中那些名词会感觉有一些熟悉,这是应该的,因为从高等数学的角度上看,函数就是实数集(或它的子集)到实数集的一个映射。形式化的说:我们设数集 \(D\subset\mathbf{R}\),则称映射 \(f:D\to \mathbf{R}\) 为定义在 \(D\) 上的函数,简记为:
\[ y=f(x),\,x\in D \]
其中 \(x\) 称为自变量,\(y\) 为因变量,\(D\) 称为函数的定义域,记作 \(D_f\) 即 \(D_f=D\)。
常见的函数有一次函数、二次函数、三角函数、对数函数等等,它们的函数图像如图。
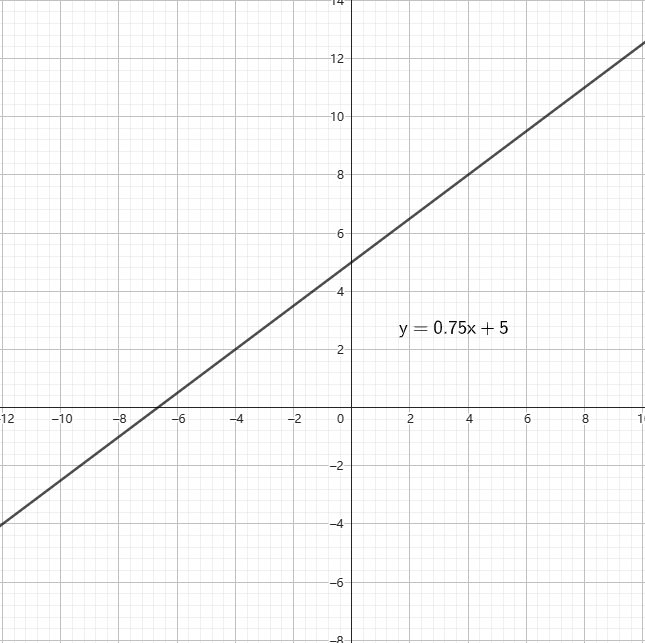
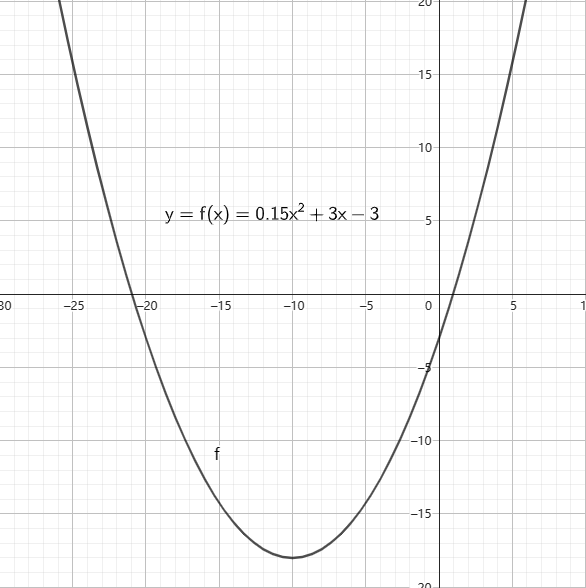
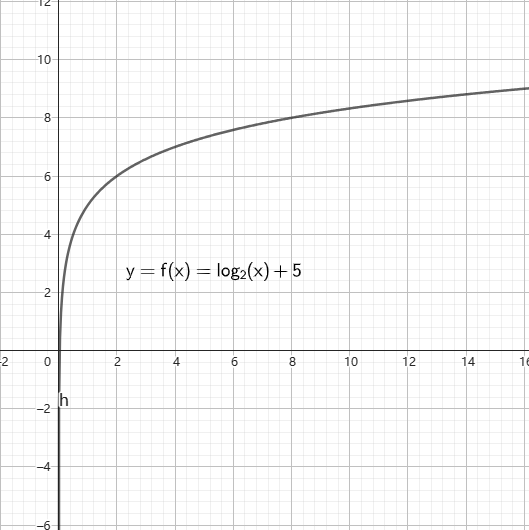
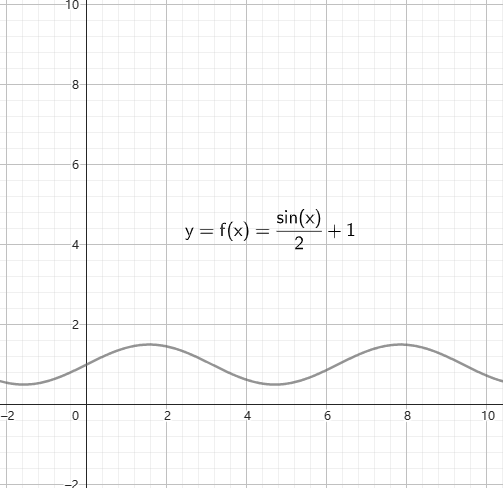
你还需要会知道一些函数的特性:
- 函数的有界性:由于函数的定义域是一定的,这可能会导致函数的值域并不是整个实数域。
- 函数的周期性:如果存在一个正数 \(l\),使得 \(f(x)=f(x + l)\) 恒成立,那么我们称这个函数为周期函数,且我们称 \(l\) 是函数 \(f\) 的周期,一般地,我们称周期为函数的。正弦函数(\(\sin\))就是常见的周期函数。
积分
积分问题通常被分为两类:不定积分和定积分。对于辛普森法,你只需要理解定积分。一般定积分以下属方式表达:
\[ \int_a^b f(x)\,\textrm{d}x \]
其中 \(b\) 为积分上限、\(a\) 为 积分下限,二者组成了一个积分区间 \([a,\,b]\)、\(f(x)\) 被称为被积函数,而 \(f(x)\,\textrm{d}x\) 称为被积表达式。
当然,聪明的你可定发现了,有些函数是不可以积分的,简称不可积。那么那些函数是可积的呢?《高等数学》告诉了我们答案:
- 设 \(f(x)\) 在区间 \([a,\,b]\) 上连续,则 \(f(x)\) 在 \([a,\,b]\) 上可积。
- 设 \(f(x)\) 在区间 \([a,\,b]\) 上有界,且只有有限个间断点,则 \(f(x)\) 在 \([a,\,b]\) 上可积。
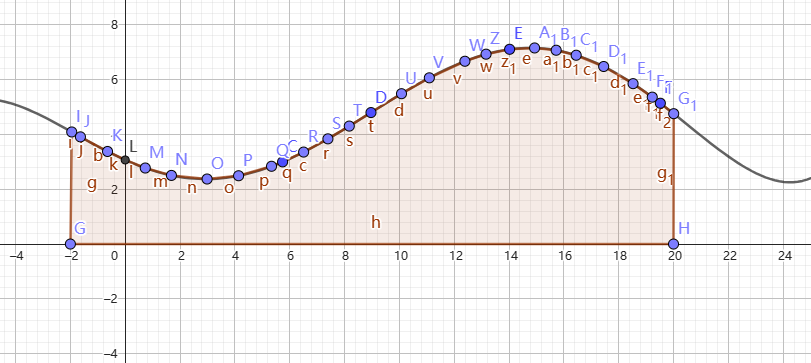
好的,那么积分是什么呢?实际上对于定积分,你可以认为他是在一段区间内函数值的和,但是这个求和是连续的,看到图3。图 3 中棕色的部分面积就是图中黑色函数在积分区间 \([-2,\,20]\) 的积分值。这就是积分的几何意义。
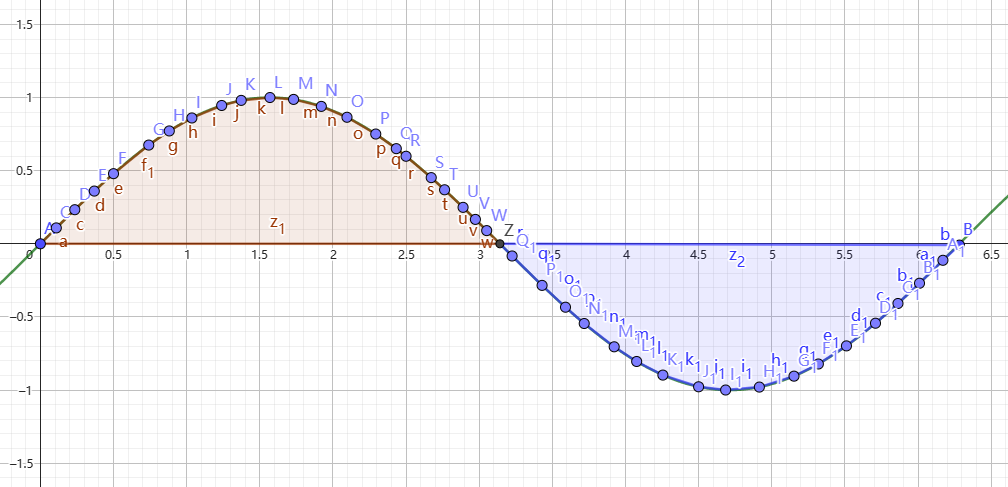
但是你可能会发现一个问题,就是如果函数在积分区间内有负值,那么怎么办呢?我么可以通过一个例子来理解这个问题。我们可以构造一个周期函数,然后尝试求他的积分值。图4就是一个正弦函数的图像。图像中棕色部分就是函数值为正的部分,区间为 \([0,\,\pi]\),蓝色部分是函数值为负的部分,区间 \([\pi,\,2\pi]\) 我们可以大胆猜测一下,函数 \(\sin (x)\) 在区间 \([0, 2\pi]\) 的积分值是棕色部分减去蓝色部分,也就是 \(0\)。拿出计算器计算一下就会发现,结论正确。定积分值实际上就是函数位于\(x\) 轴上方部分的面积减去 \(x\) 轴下方的面积!
到这里,你已经基本掌握了辛普森法所需的知识,让我们出发吧,旅行者!
思路
积分值计算
首先解决积分求值的问题,我们从最简单的矩形逼近开始。我们尝试把函数下的图形用矩形逼近,或者说常使用一些矩形把函数下的部分填满,如图5(左)。
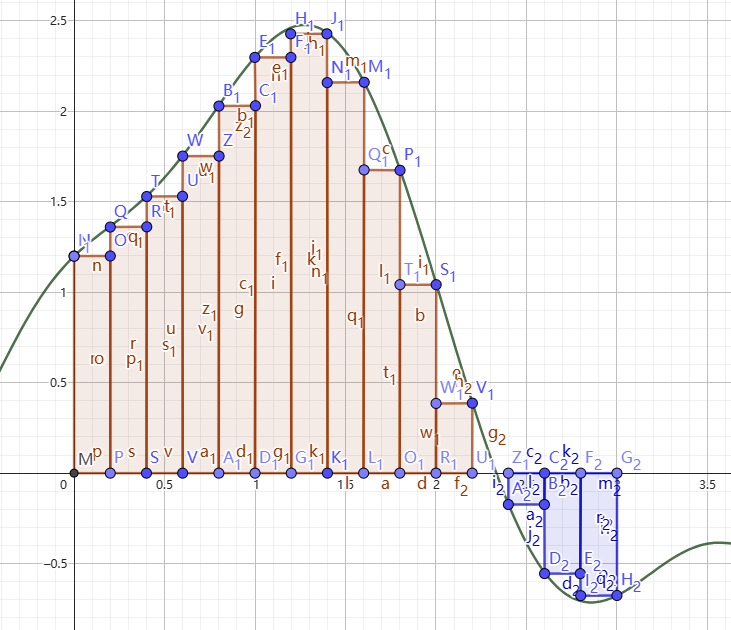
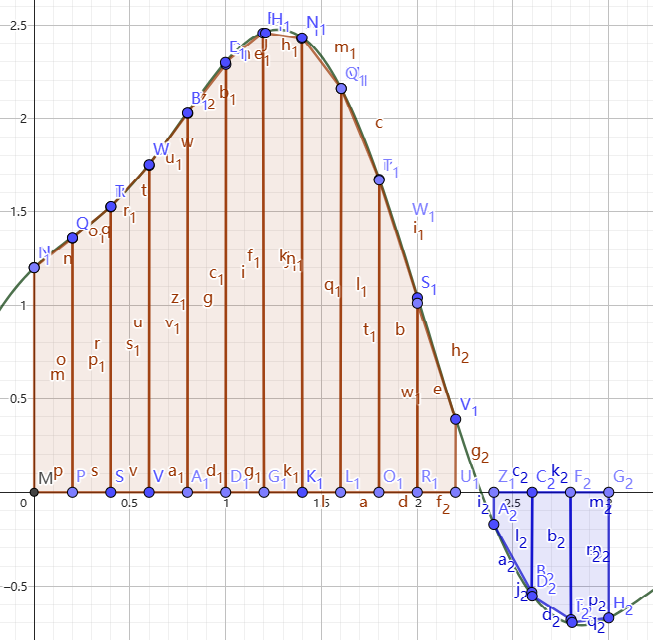
很容易发现即使我们把面积分成这么多块,精度还是十分的低。我们考虑把矩形换成梯形,就像图 5(右)。这样看起来精度似乎提升了,但是效率似乎很低,我们亟需一种高效且精度高的定积分求值方式。
如果你翻看一篇内容杂糅的论文,你就会找到一种神奇的算法:辛普森法。这种算法使用一些二次函数来逼近我们要积的函数。
原论文中对算法数学推倒的过程非常少,因此下面给出一种 Simpson 公式的非原著推导过程,我们设 \(g(x) = ax^2+bx+c\) 为拟合后的函数,则推导过程如下:
\[ \begin{align*} \int_L^R f(x)\,\textrm{d}x &\approx \frac{1}{3}a\left(R^3-L^3\right)+\frac{1}{2}b\left(R^2-L^2\right)+c\left(R-L\right)\\ &= \frac{R-L}{6}\left(2a\left(L^2+LR+R^2\right)+3b\left(L+R\right)+6c\right)\\ &= \frac{R-L}{6}\left( aL^2+bL+c+aR^2+bR+c+4a\left(\frac{L+R}{2}\right)^2+4b\left(\frac{L+R}{2}\right) + 4c\right)\\ &= \frac{R-L}{6}\left(f(L)+4f\left(\frac{L+R}{2}\right)+f(R)\right) \end{align*} \]
这就是大名鼎鼎的辛普森公式:
\[ \int_L^R f(x)\,\textrm{d}x \approx \frac{R-L}{6}\left(f(L)+4f\left(\frac{L+R}{2}\right)+f(R)\right) \]
获得了辛普森公式,正当你计算时,你就会发现精度根本不足!因为一个二次函数很显然是不足以逼近一个复杂函数的。
为了解决精度问题,我们可以考虑将函数分段,我们可以将积分区间砍半,分为两次计算。每次都将区间砍半,直到精度达标。在估算精度的过程中,还存在着一个技巧。这个技巧在《数值分析》一书中有提到。
这个技巧来源于推广中值定理[^2]。根据这个定理,我们可以发现当辛普森法算出来的积分值误差 \(\leq 15eps\) (\(eps\) 为给定的容差值(TOL)),那么这个值加上误差的 \(\frac{1}{15}\) 就是我们需要得到的足够精度的值了。具体证明参考原书 P240。
实现
下面给出【模板】自适应辛普森法 1的代码,其实就是一直二分区间直到精度达标。
1 | |
“觉得不错的话,给点打赏吧 (✿◕‿◕✿)”

微信支付

支付宝支付 (暂不支持)