算法详解 - 重链剖分

算法详解 - 重链剖分

简介

重链剖分，也被称为树链剖分，一般的，OIer 口中的树链剖分就是指重链剖分。今天我们就来一起学习重链剖分。

概念

重儿子

既然是重链剖分，那么我们就要理解什么是重。我们定义一个点的子节点中子树最大的点为这个点的重儿子。我们可以通过下面的一个例子来理解：

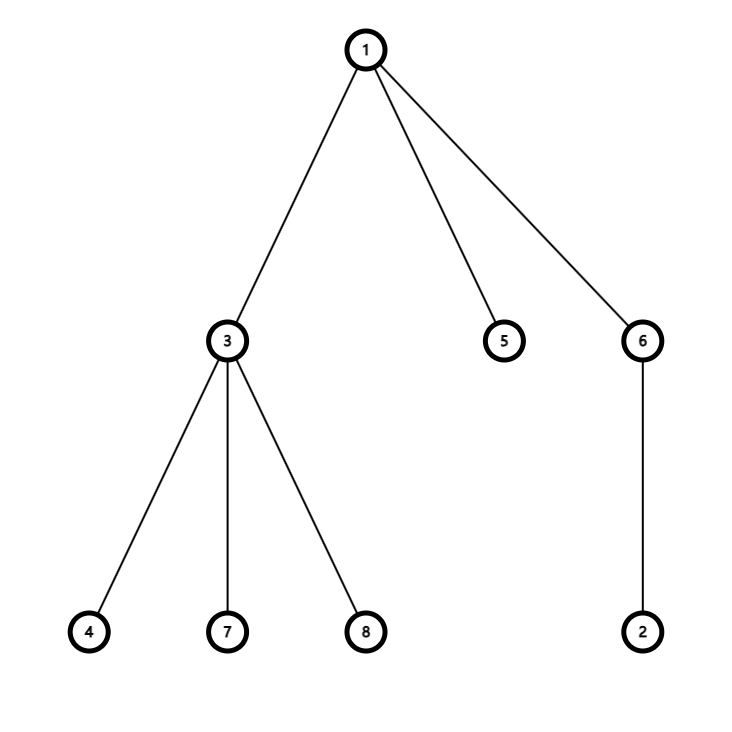
其中，节点 \(1\) 的子节点有三个，分别是 \(3,\,5,\,6\)，它们的子树大小分别是 \(4,\,1,\,2\)，于是我们按照定义可以得到节点 \(1\) 的重儿子就是子树大小为 \(4\) 的节点 \(3\)。

重链

顾名思义，重链就是重儿子所连成的链，举个例子：

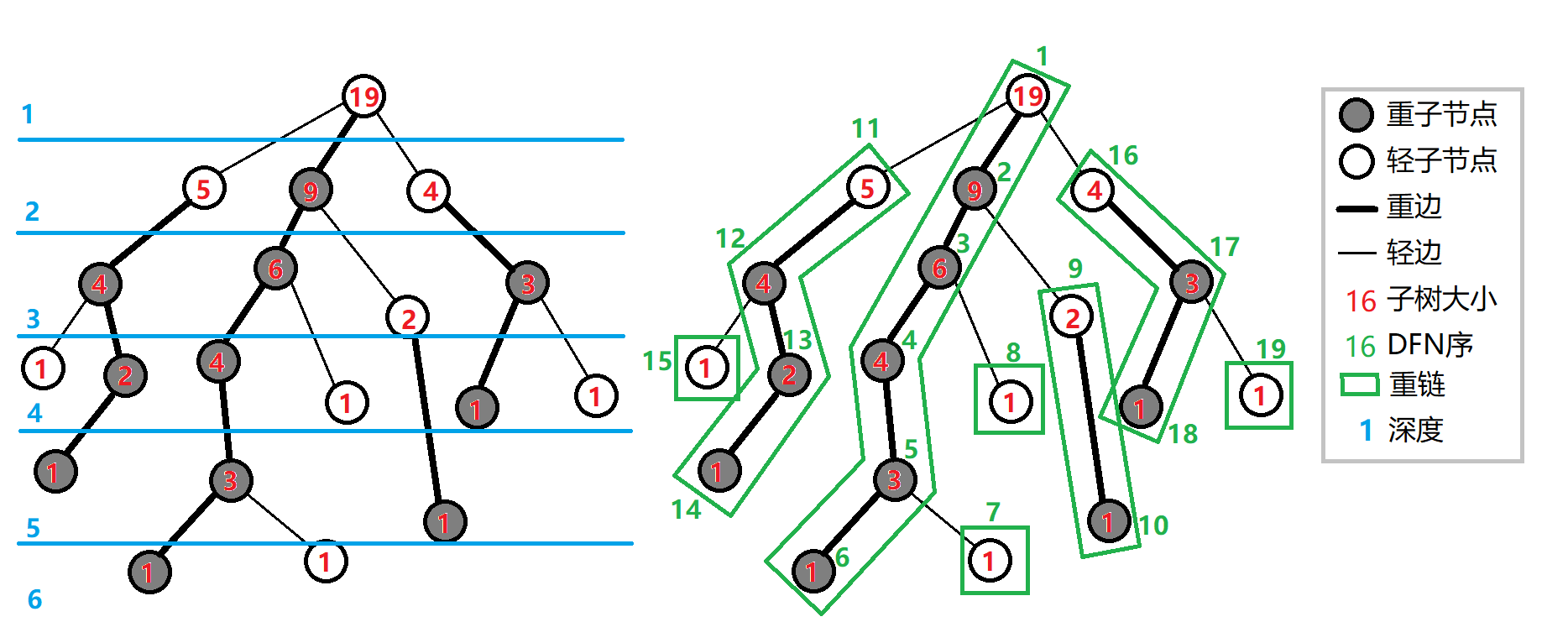
其中深色的点就是重儿子，绿色方框框起来的就是一条条重链。

实现

顾名思义，重链剖分就是把重链找出来。于是我们考虑如何找出来重链。一种很显然的方式就是进行 DFS，我们需要执行两次 DFS。

  1. 在第一次 DFS 中，我们记录出每个节点的子树大小、重儿子、深度的信息。
  2. 第二次，我们按照重儿子优先的顺序再次遍历树，然后记录 DFN 序（也就是 DFS 访问时的时间戳）以及每一条重链的重链头。

由此我们获得的这棵树的 DFN 值，但是这有什么用呢？我们需要先来了解一些性质。

性质

  • 每一个树上的节点属于且仅属于一条重链。这个其实也很好证明。由于每一个点只有一个重儿子，因此连接这个点的重链有且仅有一条。因此我们会发现重链可以把任意一棵树完全剖分（即将一棵树完全的分为若干条链）。
  • 重链内的 DFN 是连续的。这个性质很容易得到，因为我们是重度优先搜索的，因此我们必然优先搜索同一条重链上的点，于是我们同一条重链上的 DFN 就是连续的。
  • 一棵子树内的 DFN 是连续的。这个是 DFS 决定的，很好理解。你可以发现，DFS 总是遍历完当前子树再去做其他考虑，于是很容易就发现同一棵子树内的 DFN 是连续的。
  • 树上的路径可以被拆分为不超过 \(\log_2n\) 条重链。这个性质对于我们的复杂度分析是十分有用的。同时这个性质也是非常容易得到的。当我们遍历的时候，总是将子树分为重子树和其余节点，因此子树的大小总是被除以 \(2\)。

使用

我们会发现，重链剖分后 DFN 的连续性是十分可用的。这就给我们使用区间数据结构的机会了。通过这个性质，我们可以在树上借助 DFN 维护一棵线段树。线段树的下标就是对应节点的 DFN 值。

于是我们就可以动态维护一些树上的区间和、区间方差、最大最小值之类的东西，同时顺手求出 LCA，复杂度还和倍增法差距不大。

例题

思路

我们将引入一道例题以加深你对重链剖分的理解。

[NOI2015] 软件包管理器

动态维护树上的区间和。

我们看到题目给出软件包的依赖关系，很容易的就自然联想到图论上，对吧？对吧？然后我们再观察一下，发现题目刚好描述了一棵树。

我们把样例的树建出来，是这样的：

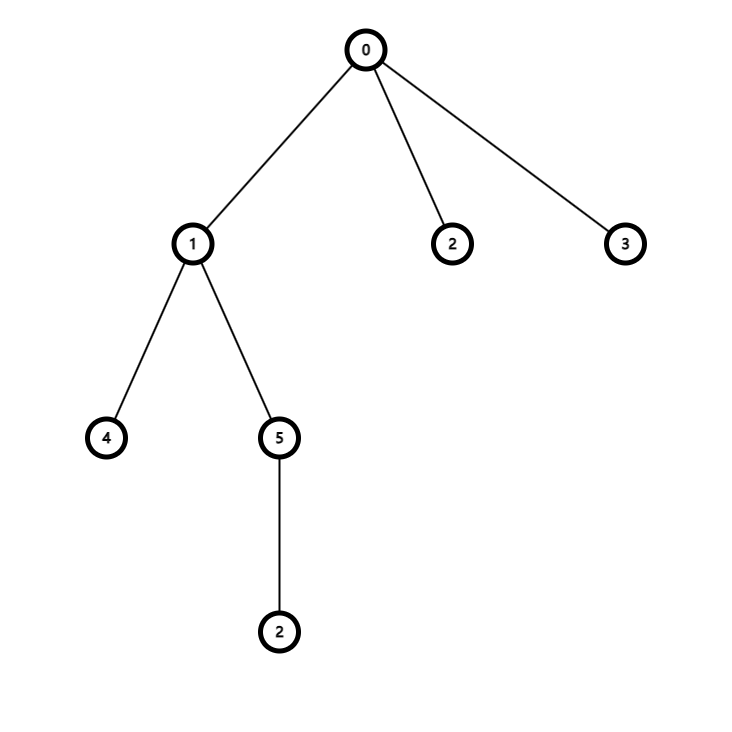
我们设每个点的初始权值为 \(0\)，也就是未安装。

  • 当安装软件包的时候，我们将该软件包到根软件包的路径上的软件包全部安装，也就是全部设置为 \(1\)，并统计有多少个原本不是 \(1\) 的，计入答案，输出。
  • 当卸载软件包时，我们卸载这个软件包及其所在子树上的软件包，也就是把整个子树都设为 \(0\)，然后统计原来有多少个 \(1\)，输出即可。

实现

我们首先用两个 DFS 预处理出我们所需的信息：深度、子树大小、重儿子、DFN 序、重链头等信息。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
void dfs1(int u, int fa) {
    sz[u] = 1; // 设置子树的大小初始为 1
    int maxn = -1; // 初始化最大子树大小
    for (int v: g[u]) {
        if (v != fa) { // 不走回头路
            f[v] = u; // 记录 v 的父亲为 u
            dep[v] = dep[u] + 1; // 记录 v 的深度为 u 的深度 + 1
            dfs1(v, u); // 遍历
            sz[u] += sz[v]; // 更新 u 的子树大小
            if (sz[v] > maxn) { // 如果发现重量更大的节点
                maxn = sz[v]; // 更新最大子树大小
                son[u] = v; // 更新重儿子
            }
        }
    }
}

void dfs2(int u, int hd, int fa) {
    head[u] = hd; // 记录重链头
    dfn[u] = ++dfncnt; // 记录 DFN 序
    if (!son[u]) { // 如果是叶子节点
        return; // 不再遍历，避免死循环
    }
    dfs2(son[u], hd, u); // 优先遍历重儿子
    for (int v: g[u]) { // 遍历轻儿子
        if (!dfn[v]) { // 如果没有遍历过
            dfs2(v, v, u); // 遍历轻儿子下去
        }
    }
}

进行预处理后，我们开始建树。

首先简单写一下线段树的两个基本操作。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
void push_up(int node) {
    tree[node] = tree[node << 1] + tree[node << 1 | 1]; // 更新子节点的数据到父节点（上传）
}

void push_down(int node, int l, int r) {
    if (tag[node] != -1) { // 如果有未下传的数据
        int mid = (l + r) >> 1;
        tag[node << 1] = tag[node]; // 下传标记，注意是直接覆盖，不是累加
        tag[node << 1 | 1] = tag[node]; // 下传标记
        tree[node << 1] = (mid - l + 1) * tag[node]; // 更新数据
        tree[node << 1 | 1] = (r - mid) * tag[node]; // 更新数据，注意是 [mid + 1, r]，区间大小 = (r - (mid + 1) + 1) = r - mid
        tag[node] = -1; // 清除未下传状态
    }
}

然后我们写一个区间修改操作。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
void update(int node, int l, int r, const int L, const int R, const int x) {
    if (L <= l && r <= R) { // 如果遍历到的区间被待修改区间包含
        tag[node] = x; // 直接修改
        tree[node] = (r - l + 1) * x;
        return;
    }
    push_down(node, l, r); // 下传标记
    int mid = (l + r) >> 1;
    if (L <= mid) { // 如果左儿子与待修改区间有交集
        update(node << 1, l, mid, L, R, x); // 修改
    }
    if (R > mid) { // 如果右儿子与带修改区间有交集
        update(node << 1 | 1, mid + 1, r, L, R, x); // 修改
    }
    push_up(node); // 上传修改
}

然后类似地写一个区间查询。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
int query(int node, int l, int r, const int L, const int R) {
    if (L <= l && r <= R) { // 如果当前区间被待查区间完全包含
        return tree[node]; // 返回值
    }
    push_down(node, l, r); // 下传标记
    int mid = (l + r) >> 1, ans = 0;
    if (L <= mid) { // 如果左儿子与待查询区间有交集
        ans += query(node << 1, l, mid, L, R); // 统计答案
    }
    if (R > mid) { // 如果右儿子与待查询区间有交集
        ans += query(node << 1 | 1, mid + 1, r, L, R); // 统计答案
    }
    return ans;
}

然后我们来看一下如何遍历某一个节点到 \(1\) 节点的路径，我们考虑类似 LCA 的方法往上跳，实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
int ans = 0;
while (head[x] != head[y]) { // 如果还没到
    if (dep[head[x]] < dep[head[y]]) { // 优先跳较深的节点，于是判断一下
        swap(x, y);
    }
    ans += query(1, 1, n, dfn[head[x]], dfn[x]); // 统计答案
    x = f[head[x]]; // 将较深的节点调到重链头的父节点
}
if (dep[x] > dep[y]) { // 让较浅的节点是 x，而较深的节点为 y，方便后续操作
    swap(x, y);
}
ans += query(1, 1, n, dfn[x], dfn[y]); // 统计二者之间路径的答案

当然在我们的题目中，\(y\) 始终不变，于是乎我们可以将这段代码简化一下，就像这样（加上了修改的过程，注意先查再改）：

1
2
3
4
5
6
7
8
int ans = dep[x] + 1; // 初始时假定整条路径都没有安装
while (head[x] != head[1]) {
    ans -= query(1, 1, n, dfn[head[x]], dfn[x]); // 减去已安装的
    update(1, 1, n, dfn[head[x]], dfn[x], 1); // 修改
    x = f[head[x]]; // 更新
}
ans -= query(1, 1, n, dfn[1], dfn[x]); // 减去已安装
update(1, 1, n, dfn[1], dfn[x], 1); // 更新

此时我们的 ans 就是所要求的需要额外安装的节点数量啦。

然后我们来考虑如何更新子树上的东西。我们在刚刚提到了一个性质：一棵子树内的 DFN 是连续的，于是利用这个性质，我们可以很容易的得出区间。假设子树的根节点是 \(u\)，那么这个子树 DFN 序最小的必然就是根节点了，又由于子树内下标连续，因此我们可以计算出最后一个属于子树的下标是 \(dfn_u + sz_u - 1\)（根节点 DFN + 字数大小 - 1）。这样我们就可以很快的统计出答案啦！

1
2
cout << query(1, 1, n, dfn[x], dfn[x] + sz[x] - 1) << endl;
update(1, 1, n, dfn[x], dfn[x] + sz[x] - 1, 0);

最后贴一下整体的代码，希望你喜欢这篇文章呀：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
#include <iostream>
#include <vector>
#include <cstring>

#define endl '\n'

using namespace std;

int n, q, dfncnt, tree[400009], tag[400009], dep[100009], head[100009], dfn[100009], f[1000009], sz[100009], son[100009];
vector<int> g[100009];

void dfs1(int u, int fa) {
    sz[u] = 1;
    int maxn = -1;
    for (int v: g[u]) {
        if (v != fa) {
            f[v] = u;
            dep[v] = dep[u] + 1;
            dfs1(v, u);
            sz[u] += sz[v];
            if (sz[v] > maxn) {
                maxn = sz[v];
                son[u] = v;
            }
        }
    }
}

void dfs2(int u, int hd, int fa) {
    head[u] = hd;
    dfn[u] = ++dfncnt;
    if (!son[u]) {
        return;
    }
    dfs2(son[u], hd, u);
    for (int v: g[u]) {
        if (!dfn[v]) {
            dfs2(v, v, u);
        }
    }
}

void push_up(int node) {
    tree[node] = tree[node << 1] + tree[node << 1 | 1];
}

void push_down(int node, int l, int r) {
    if (tag[node] != -1) {
        int mid = (l + r) >> 1;
        tag[node << 1] = tag[node];
        tag[node << 1 | 1] = tag[node];
        tree[node << 1] = (mid - l + 1) * tag[node];
        tree[node << 1 | 1] = (r - mid) * tag[node];
        tag[node] = -1;
    }
}

void update(int node, int l, int r, const int L, const int R, int x) {
    if (L <= l && r <= R) {
        tag[node] = x;
        tree[node] = (r - l + 1) * x;
        return;
    }
    push_down(node, l, r);
    int mid = (l + r) >> 1;
    if (L <= mid) {
        update(node << 1, l, mid, L, R, x);
    }
    if (R > mid) {
        update(node << 1 | 1, mid + 1, r, L, R, x);
    }
    push_up(node);
}

int query(int node, int l, int r, const int L, const int R) {
    if (L <= l && r <= R) {
        return tree[node];
    }
    push_down(node, l, r);
    int mid = (l + r) >> 1, ans = 0;
    if (L <= mid) {
        ans += query(node << 1, l, mid, L, R);
    }
    if (R > mid) {
        ans += query(node << 1 | 1, mid + 1, r, L, R);
    }
    return ans;
}

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);
    cin >> n;
    for (int i = 2, x; i <= n; i++) {
        cin >> x;
        x += 1;
        g[x].push_back(i);
        g[i].push_back(x);
    }
    memset(tag, -1, sizeof tag);
    dfs1(1, 0);
    dfs2(1, 1, 0);
    cin >> q;
    string op;
    for (int i = 1, x; i <= q; i++) {
        cin >> op >> x;
        x += 1;
        if (op == "install") {
            int ans = dep[x] + 1;
            while (head[x] != head[1]) {
                ans -= query(1, 1, n, dfn[head[x]], dfn[x]);
                update(1, 1, n, dfn[head[x]], dfn[x], 1);
                x = f[head[x]];
            }
            ans -= query(1, 1, n, dfn[1], dfn[x]);
            update(1, 1, n, dfn[1], dfn[x], 1);
            cout << ans << endl;
        } else if ("uninstall") {
            cout << query(1, 1, n, dfn[x], dfn[x] + sz[x] - 1) << endl;
            update(1, 1, n, dfn[x], dfn[x] + sz[x] - 1, 0);
        }
    }
}
算法详解
#算法详解 #重链剖分
算法详解 - 重链剖分
https://lixuannan.github.io/posts/9181.html
作者
CodingCow Lee
发布于
2024年4月8日
许可协议