TYOI 暑假集训游记
比赛复盘
分数
| 比赛 | 排名 | 分数 | 是否意外 |
|---|---|---|---|
| 2023 tyoi 普及模拟训练 01 | \(21\) | \(150\) | 是 |
| 2023 tyoi 普及模拟训练 02 | \(30\) | \(220\) | 是 |
| 2023 tyoi 普及模拟训练 03 | \(13\) | \(260\) | 否 |
| 2023 tyoi 普及模拟训练(B --> C) | \(5\) | \(180\) | 是 |
| 2023 tyoi 普及模拟训练 04 | \(17\) | \(196\) | 是 |
| 2023 tyoi 普及模拟训练 05 | \(8\) | \(420\) | 否 |
| 2023 tyoi 普及模拟训练 06 | \(15\) | \(123\) | 否 |
| 2023 tyoi 普及模拟训练 07 | \(20\) | \(160\) | 是 |
| 2023 tyoi 普及模拟训练(B --> C)(LJY) | \(8\) | \(310\) | 否 |
| 2023 tyoi 普及模拟训练 08 | \(21\) | \(110\) | 是 |
| 2023 tyoi 普及模拟训练 09 | \(7\) | \(220\) | 否 |
| 平均 | - | \(213.54\) | |
| 总和 | - | \(2349\) |
感受
对于前两场比赛,由于太久没有参加比赛,对比赛的节奏和手感各方面掌握的不是很好。有一些非常简单的解法并没有想到,分数和排名还算是比较意外。但是有一题让我印象很深刻,2023 tyoi 普及模拟训练 02 T2,这道题很有意思,比赛结束后我发现了我的解法和其余所有人的解法几乎都不相同,但竟然也是对的(\(\Huge 大喜\))
从第三场比赛开始,打比赛的时候就比较有感觉,对于题目的理解就越发深刻,对于自己的成绩,我个人还是认为还算合格。但是这几场比赛下来有一些小问题,还是需要总结一下:
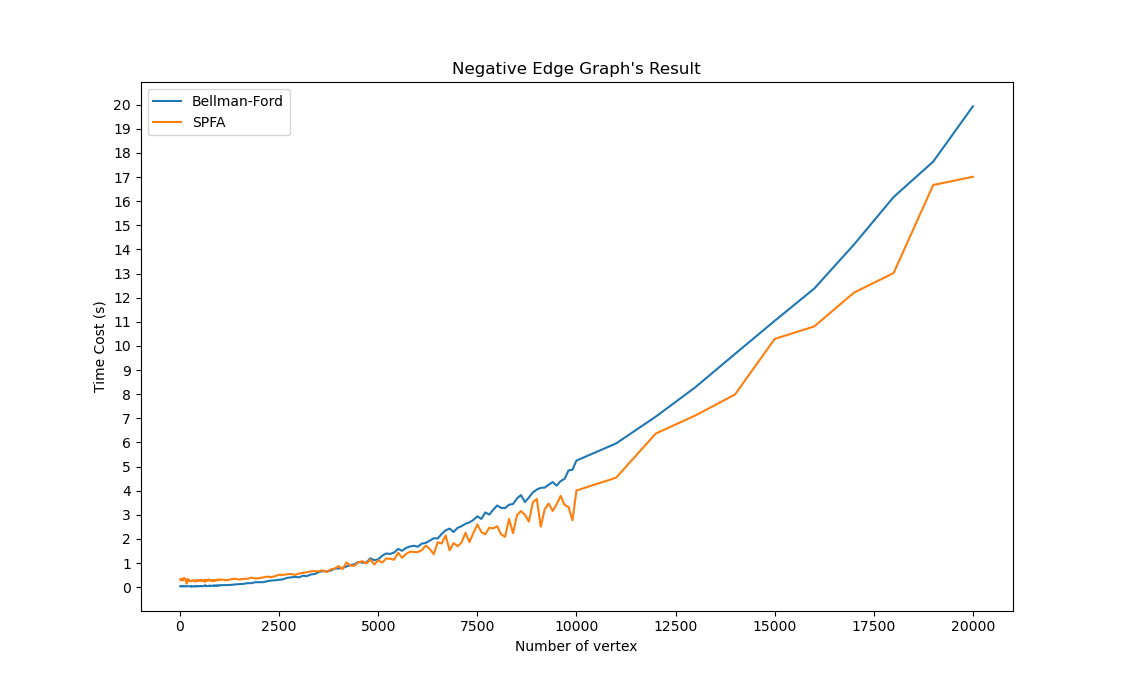
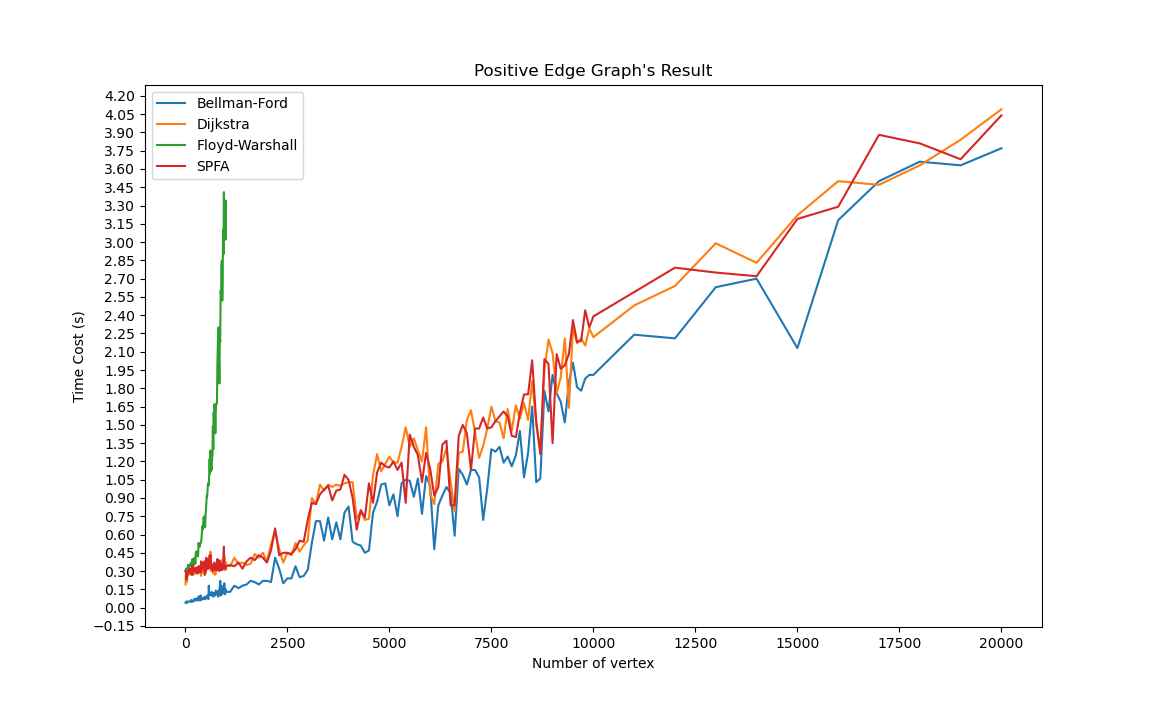
- 对于算法的选择:在最短路算法中,如果有负权环,应当选用在数据量大时效率更高的
SPFA 算法(比较见图一),而在没有负权环的图中,对于较为稀疏的图,应使用
Bellman-Ford 算法(比较见图二),而稠密图中 Dijkstra
是更优的选择(没图了)
- 还有就是输入输出的问题,在 2023 tyoi 普及模拟训练
05 中,T3 由于使用了
endl作为换行,但疏忽了endl在换行的同时会刷新缓冲区,从而导致时间超限。后来通过#define endl '\n'重载了endl的内容,使得endl不再刷新缓冲区,解决时间超限的问题
在最后一周的比赛中,有两场比赛让我感到有些意外,也有些可惜。在 2023 tyoi 普及模拟训练 08 中,T3 是很让我遗憾的一道题。在赛时我看到题的第一反应就是分层图最短路,火速打完之后发现却连样例都过不了。查看调试信息后发现最短路计算中所选取的路径存在复用关系的情况,因此会导致答案偏小。在答案错误后,我曾有想过使用题目的正解\(\rightarrow\)最小生成树,但是我很快否决了这个想法(\(\tiny 我是扇贝\)),后又想到了贪心,但由于打不出来,最终交上去了分层图最短路的代码,\(0\ pts\) \(\Huge 寄\) 。 还有一场比赛就是 2023 tyoi 普及模拟训练 07 ,在这场比赛里,我成功的把前缀和 + 枚举的入门红打成了调得半死的一维 DP,还爆零啦,再次 \(\tiny 我是扇贝\)
总而言之,这三个星期的模拟赛还是给了我不小的提升的,让我学到了很多新知识,也给我的未来学习指引了一些方向,是我受益匪浅。
新知识
这次集训所学习的新知识并不多,主要都与图论相关。就我自身而言,我认为难度最高的是割点与桥的应用,毕竟你很难看出那道题是割点与桥的应用(好像说了跟说了一样)。最为简单的应该是差分约束系统,这也是一个很巧妙的系统。下面简单概括一下各个知识点。
- 差分约束系统。差分约束系统是一个很巧妙的东西。在数学中,这个东西被表示为一个不等式集,就像这样 \(\left\{\begin{array}{lc}x_1 - x_2 \le c_1 \cr x_2 - x_3 \le c_2 \cr \vdots \ \ \ \ \ \ \ \ \ \vdots \ \ \ \ \ \ \ \ \vdots \cr x_{n - 2} - x_{n - 1} \le c_{n - 1} \cr x_{n - 1} - x_{n} \le c_n\end{array}\right.\) 而这个不等式组稍微移项一下又可以变成这样 \(\left\{\begin{array}{lc}x_1 \le c_1 + x_2 \cr x_2 \le c_2 + x_3 \cr \vdots \ \ \ \ \ \ \ \ \ \vdots \ \ \ \ \ \ \ \ \vdots \cr x_{n - 2} \le c_{n - 1} + x_{n - 1} \cr x_{n - 1} \le c_n + x_{n}\end{array}\right.\) ,这就和最短路算法中的松弛过程的条件很相似,那么我们是否可以使用常见的最短路算法(Dijkstra、SPFA)来解决这个问题呢?答案是肯定的,只需要根据约束条件建图,再跑一遍最短路算法,你就可以求得一组可能的解(无解情况除外),我想说,这真的 \(\Huge 泰裤辣\) 。
- 强联通分量。强联通分量是一个图论中的概念,他的定义是有向图中的极大强联通子图,而强联通意为图中任意两点都互相可达。 对于求强联通分量的算法主要是有美国计算机科学家 Robert E. Tarjan (罗伯特·塔扬,1948 ~ 今)提出的 Trajan 算法,这个算法基于深度优先搜索(DFS),在深度优先搜索的同时记录两个数组 \(dfn\) 以及 \(low\) ,这两个数组的定义分别是 DFS 时间戳以及该节点的多有子节点以及该节点的 \(dfn\) 的最小值。而当一个节点的 \(dfn\) 值和 \(low\) 值相同时,该节点与该节点的所有子节点构成了一个极大的强联通子图即强联通分量。强联通分量还有一个很著名的应用 \(\rightarrow\) 缩点。在有的时候,你往往需要计算一个图的连通性相关的内容,而此时由于强联通分量内部任意两点都互相可达,我们可以直接将一个强联通分量看做一个节点,并进行所需要的计算,这个过程被称为缩点。
- 割点与桥。割点与桥是无向图中关于连通性的两个概念,割点的定义是如果把一个点删除后这个图的极大连通分量数增加了,那么这个点就是这个图的割点,而桥的定义是对于一个无向图,如果删掉一条边后图中的连通分量数增加了,则称这条边为桥或者割边。求割点与桥的算法也是由美国计算机科学家 Robert E. Tarjan (罗伯特·塔扬,1948 ~ 今)提出的(Orz 大奆)。与求强联通分量基本一致,不详细展开。
- 并查集。并查集是一种很高级的数据结构。本质上并查集是一堆集合的集合,这个集合的集合支持两个操作:合并(Union)、查询(Find)。所以这个集合的集合的名字就是并查集(好草率)。并查集的时间复杂度是极其优秀的,查询的时间复杂度为 \(\Theta\left(\alpha\left(n\right)\right)\) (其中 \(n\) 为集合中的元素数量),而合并的复杂度是 \(\Theta\left(1\right)\) (已知祖先的情况下)。实现这样的复杂度还要仰赖于路径压缩,即在搜索的同时将一个子集内所有元素的祖先设为该集合的公共祖先。而该算法的时间复杂度分析是由 Tarjan 大奆提出的 (\(\Huge \%\) 他真的我哭死,图论创始人是吧,欧拉的墓都让他刨了)基于并查集,我们可以实现一些很不错的功能,比如判断图的连通性或者记录图中连通块的数量等等。
- 最小生成树。最小生成树(MST, Minimum Spanning Tree) 是一种比较特殊的树,他的定义是边权和最小的生成树。这种树在电路板布线、路由设计等领域很有用处。常见的 MST 算法有 Kruskal 和 Prim 。其中 Kruskal 算法是一种基于贪心策略的算法,算法会对所有边按边权升序排序,然后对于不与最小生成树联通的边,将其加入最小生成树,当加入的节点构成了一棵树时,这棵树就是我们希望求得的最小生成树。
学习状态
这三个星期的学习状态我个人认为还是不错的,态度较为认真。在这三个星期的集训中学到了不少知识,同时在比赛中锻炼了自己的比赛状态和应对题目的能力。和同学在一起生活、交流,也让我受益匪浅,在了解同学趣事的同时,也互相进行了很多技术和能力上的交流,大家都无比换了的度过了难得的集训时光。
课余
每天下午下课,我们总会结伴来到操场,或足球,或篮球。一切的体育运动在我们的眼中都是充满趣味和激情的。
集训结束前最后一天,我们 ABC 三个班的同学加上一位隔壁物理队的同学共 \(22\) 人在绿茵场上挥洒汗水。慷慨淋漓的打了离开越秀校区前的最后一场球赛。在这场球赛中我们虽败由乐,赛后大家都欢声笑语的走回科技楼,在笑声中结束了为期三周的集训。
在这为期三周的集训中,出现了不少好 van 的东西:
- DLT 计数法:一两二三四,五六拐八九
- 想成功,先发疯,不顾一切向前冲,今天睡地板,明天
睡老板,加油!!!加油!!!加油!!!。 - 真正的小丑:玩家:“游戏结束,小丑胜利”;法官:“游戏继续,天黑请闭眼”(小丑被盗宝偷了,哈哈哈哈我能笑两年半)
- CYY 的 Hack 数据
对老师
感觉没什么好说的,都挺好的,O(∩_∩)O 哈哈~
“觉得不错的话,给点打赏吧 (✿◕‿◕✿)”

微信支付

支付宝支付 (暂不支持)