MCOI 2023年6月月赛题解

MCOI 2023 年 6 月月赛题解

引言

这是一场个人认为难度 \(\approx\) J- 级的比赛，除了最后一题是一道非常怪的题以外其他的题目都是比较简单的，但是会有一些坑。由于出题人写 TJ 的时候你们的比赛还没有结束，因此没法评价本场比赛。个人估计应该不会有人 AK，但是这场比赛应该 \(300\) pts 的巨佬不少。下面是各题的题解，写的不好，请多多关照。

T1 - WTX 的文采

思路

首先要理解一下题意，出题人保守估计大部分做不出此题的选手是因为看不懂题目里面的式子。所以让我们来看一下这个式子：

\[ y_i=\left(\displaystyle\sum_{j=l_i}^{r_i}\ [z_j\ge w]\ 1\right)\times\left(\displaystyle\sum_{j=l_i}^{r_i}\ [z_j\ge w]\ p_j\right) \]

首先我们可以将这个式子按照乘号分成两个部分，我们先行理解左边的部分 \(\sum_{j=l_i} ^ {r_i}\ [z_j \ge w]\ 1\) 首先我们理解一下这个符号 \(\sum\) （西格玛，念做：sigma ['sigma] ）。实际上就是一个求和，或者理解为一个 for 循环，\(\sum\) 符号下面的是循环变量的起始值，然后上面的那个数是循环变量的最大值，循环变量每次加一，然后右边的 \([]\) 里面的内容是后面算式是否累加的条件，也就是说，这个西格玛可以变成下面的一段伪代码（伪代码格式参考《算法导论》（英文名 Intrudution to Algorithms））：

\[ \begin{array}{l} ans = 0\\ for\ j\ = l_i\ to\ r_i\\ \ \ \ \ if\ z_j \ge w\\ \ \ \ \ \ \ \ \ ans += 1\\ \end{array} \]

同理，我们可以理解第二块式子的意思，那么就很简单了。

为了优化多次查询，我们可以写两个前缀和数组，分别是第一块和第二块式子的结果，然后进行查询，计算出结果并输出。

如果不理解前缀和，可以查看 oi-wiki 的讲解

标程

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#include <iostream>

using namespace std;

unsigned long long n, m, w, x, z[10000009], p[10000009], l, r, y;

int main() {
    cin >> n >> m >> w;
    for (int i = 1; i <= n; i++) {
        cin >> x >> p[i];
        if (x >= w) {
            p[i] += p[i - 1];
            z[i] = z[i - 1] + 1;
        } else {
            p[i] = p[i - 1];
            z[i] = z[i - 1];
        }
    }
    for (int i = 1; i <= m; i++) {
        cin >> l >> r;
        if (l > r) {
            swap(l, r);
        }
        cout << (z[r] - z[l - 1]) * (p[r] - p[l - 1]) << endl;
    }
}

T2 - WTX 的蛋糕

思路

首先我们抽象一下题目，在一个三维空间内，有一个无穷大的物体，同时有一条直线，用这条将这个物体切成若干份，求切 \(n\) 刀后这个三维空间内的物体的块数。由于题目中并没有说明物体是否可移动，所以我们假定物体是可以移动的，因为这样可以使物体的块数最大化。

我们考虑对一块完整的物体的情况，很显然，一刀最多把它切成两块。不能再多了，因为再多一点就快爆炸。那么我们如果在每次切完之后将物体摆放好，使得每一小块都可以被这条直线切到，那么我们就实现的小块的数量最大化。由于我们只能切 \(n\) 刀，所以我们可以发现，物体的最多数量是 \(2 ^ n\) ，那么这就很简单了，对吧？

不对！！！我们观察一下题目的数据范围，达到了惊人的 \(10 ^ {18}\) 。要知道，c++ 语言内置的最大的整数数据结构 __int128 也只能存储 \(2 ^ {128}\) 啊，这 \(2 ^ {1e18}\) 要怎么存呢？

再多看一眼就快爆炸题目就可以发现题目非常良心的让我们将最终结果对一个很大的质数 \(1e9 + 7\) 取模，也就是说不会产生数据溢出的情况，但是因为这个模数的存在，我们无法调用 STL 函数 pow(int n, int m) 所以我们需要自己写一个幂函数。

但是话又说回来，这个幂函数采用通常的写法时间是肯定会超限的，因为常规的幂函数写法时间复杂度是线性的 \(O(n)\) ，很显然，对于 \(10 ^ {18}\) 来说，这个运算至少需要 \(2000\ ms\) 才能完成，但是题目的时间限制只有 \(250\ ms\) ，是当前算法的 \(4\) 倍有余。那这该怎么办呢？

这时候我们需要引入一个算法：快速幂（ quick power )

首先我们看一个例子：\(2 ^ {10}\) ，我们按照算式展开应该是这样的 \(\underbrace {2 \times 2 \times...\times2\times2} _{10\ 个\ 2}\) 那么有没有一种方法可以减少一下运算呢，我们会发现，\(2 ^ {10}\) 应该是等于 \(2 ^ {5} \times 2 ^ {5}\) 的，折这一点上过小学二年级应该都知道，那么我们只需要计算 \(2 ^ 5\) 就可以了，以此类推，我们就会发现，实际上我们只需要进行最多 \(\lfloor\log_2n\rfloor + 1\) 次运算就可以计算出来 \(2 ^ n\) 的精确数值，这种思路在算法导论中被称为分治。下面介绍两种快速幂的实现思路

快速幂思路 1

使用递归实现分治算法，伪代码如下：

\[ \begin{array}{l} QUICK\_POW(a, b, m)\\ \ \ \ \ if\ b\ == 0\\ \ \ \ \ \ \ \ \ return\ 1\\ \ \ \ \ if\ b\ ==\ 1\\ \ \ \ \ \ \ \ \ return\ a\ \%\ m\\ \ \ \ \ temp = QUICK\_POW(a, \lfloor b\ ÷\ 2 \rfloor, m)\ \%\ m\\ \ \ \ \ if\ b\ \%\ 2==1\\ \ \ \ \ \ \ \ \ return\ (temp \times temp \times a)\ \%\ m\\ \ \ \ \ return\ (temp \times temp)\ \%\ m \end{array} \]

这种方法实现思路较为简单，直接模拟即可，但是这种算法由于递归的存在，时间上不如递推算法，同时对空间的要求比较高，如果遇见特别大的指数，有可能爆栈

快速幂思路 2

使用递推的方式实现分治算法，伪代码如下：

\[ \begin{array}{l} QUICK\_POW(a, b, m)\\ \ \ \ \ ans = 1\\ \ \ \ \ while\ b>0\\ \ \ \ \ \ \ \ \ if\ b\ \%\ 2\ ==\ 1\\ \ \ \ \ \ \ \ \ \ \ \ \ ans=(ans \times a)\ \%\ m\\ \ \ \ \ \ \ \ \ a = (a \times a)\ \%\ m\\ \ \ \ \ \ \ \ \ b = \lfloor b\ ÷\ 2\rfloor\\ \ \ \ \ return\ ans\ \%\ m \end{array} \]

这种代码书写方法在内存占用上较为优秀，同时时间上用于没有调用栈的操作，更快一些。

根据上面的思路，只需要将其用你熟练的语言实现一下即可

标程

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#include <iostream>

#define int long long

using namespace std;

int qpow(int x, int p, int m) {
    int ans = 1;
    while (p) {
        if (p & 1) {
            ans = (ans * x) % m;
        }
        x = (x * x) % m;
        p >>= 1;
    }
    return ans % m;
}

int n, ans;

signed main() {
    cin >> n;
    ans = qpow(2, n, 1000000007);
    cout << ans;
}

T3 - WTX 的追逐

思路

这道题显然很简单，是一个单源最短路问题，但是终点的选的有点奇怪，如果是 t 或者 c 就是终点，也就是说这道题没有办法使用双向广搜或者A*算法之类极其高效的算法，由于又存在障碍物，所以我们也不能使用贪心优先搜索（ GBFS ）这种虽然快但是有可能不准确的算法，我们剩下两种寻路算法：广度优先搜索（ BFS ）和深度优先搜索（ DFS ）。下面我们分析这两种算法的可行性和性能。

对深度优先搜索分析

首先我们观察一下深度优先搜索的特性，这里引用我们 TYOI 一位老队员的比喻：深搜就像一头牛，不撞南墙不回头 。根据这句话，我们可以发现深度优先搜索似乎在找到最短路径之前有可能花费很多时间进行其他路线的寻找，这将浪费很多时间。同时因为深度优先搜索通常是使用递归实现的，这种算法在矩阵很大很大的情况下可能会出现内存超限或者爆栈的情况。不过 DFS 也不是完全没有优点，对于这道题或者其他需要输出路径的情况，递归的调用方式对输出路径来说更加的方便。综上所述，深度优先搜索并不适合此题，不过，良心的出题人为使用 DFS 的选手准备了 \(25\ pts\) 的部分分，感动吧。┭┮﹏┭┮

对广度优先搜索分析

我们首先再次观察一下广度优先搜索的特性，我们会发现，广度优先搜索有点像洪水（ flood ），会匀速的蔓延到四周的节点。根据这个特性，我们会发现，BFS 找到的第一条路径一定是最短的路径之一，所以我们在找到第一条路径的时候就可以退出搜索，然后输出路径。但是这种算法对于记录路径来说会有一些困难。不过如果你学过树结构的存储的话，你会发现我们可以借鉴树的存储方法，使用一个二维数组 father[][] 来记录每一个节点的前驱。用这种方法来记录一条可行的路径，但是你需要注意的是起点的前驱应当设置为一个奇怪的值，比如一个不可能出现的点的坐标，如：\((-1, -1)\) 。

接下来是实现的方法，下面给出两个关键的函数的伪代码，首先是广搜函数：

\[ \begin{array}{l} a[n][m] = map\\ vis[n][m] = a\ array\ mark\ which\ point\ has\ been\ walked\ and\ which\ not\\ s.x = starting\ point's\ x\ axis\\ s.y = starting\ point's\ y\ axis\\ x\_axis\_ofset=[0, 0, -1, 1]\\ y\_axis\_ofset=[-1, 1 , 0, 0]\\ BFS()\\ \ \ \ \ q.push(s.x, s.y)\\ \ \ \ \ father[s.x][s.y] = \{-1, -1\}\\ \ \ \ \ while\ not\ q.empty()\\ \ \ \ \ \ \ \ \ front=q.front()\\ \ \ \ \ \ \ \ \ if\ a[front.x][front.y] == 'C'\ or\ a[front.x][front.y] == 'T'\\ \ \ \ \ \ \ \ \ \ \ \ \ OUTPUT(front.x, front.y)\\ \ \ \ \ \ \ \ \ \ \ \ \ return\\ \ \ \ \ \ \ \ \ for\ i=0\ to\ 3\\ \ \ \ \ \ \ \ \ \ \ \ \ x\_next=front.x+x\_axis\_ofset[i]\\ \ \ \ \ \ \ \ \ \ \ \ \ y\_next=front.y+y\_axis\_ofset[i]\\ \ \ \ \ \ \ \ \ \ \ \ \ if\ not\ (a[x\_next][y\_next]=='\#'\ or\ vis[x\_next][y\_next])\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ q.push(\{x\_next,y\_next\})\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ vis[x\_next][y\_next]=true\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ father[x\_next][y\_next] = front\\ \end{array} \]

其次是输出函数：

\[ \begin{array}{l} father[n][m]=a\ array\ storage\ the\ father\ of\ a\ point\\ OUTPUT(x, y)\\ \ \ \ \ if\ x==-1\ and\ y==-1\\ \ \ \ \ \ \ \ \ return\\ \ \ \ \ OUTPUT(father[x][y].x, father[x][y].y)\\ \ \ \ \ if\ father[x][y].x == -1\ and\ father[x][y].y==-1\\ \ \ \ \ \ \ \ \ PRINT("(\%d,\ \%d)",\ x,\ y)\\ \ \ \ \ else\\ \ \ \ \ \ \ \ \ PRINT("(\%d,\ \%d)\ ->\ ",\ x,\ y)\\ \end{array} \]

剩下的部分就是输入和一些简单的处理了，大家可以用自己喜欢的语言实现一下

标程

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
#include <iostream>
#include <queue>

using namespace std;

struct point {
    int x, y;

    inline bool operator==(const point a) const {
        return a.x == x && a.y == y;
    }
};

int r, c, l, xx[] = {-1, 1, 0, 0}, yy[] = {0, 0, -1, 1};
point s, t, father[109][109];
char a[109][109];
bool vis[109][109];
queue<point> q;

void out(int x, int y) {
    if (father[x][y] == (point) {-1, -1}) {
        printf("(%d, %d) -> ", x, y);
        return;
    }
    out(father[x][y].x, father[x][y].y);
    if (x == t.x && y == t.y) {
        printf("(%d, %d)", x, y);
    } else {
        printf("(%d, %d) -> ", x, y);
    }
}

void bfs() {
    q.push(s);
    vis[s.x][s.y] = true;
    father[s.x][s.y] = (point) {-1, -1};
    while (!q.empty()) {
        point front = q.front();
        q.pop();
        if (a[front.x][front.y] == 'T' || a[front.x][front.y] == 'C') {
            t.x = front.x, t.y = front.y;
            out(front.x, front.y);
            return;
        }
        for (int i = 0; i < 4; i++) {
            int x = front.x + xx[i], y = front.y + yy[i];
            if (x <= 0 || y <= 0 || x > r || y > c || vis[x][y] || a[x][y] == '#') {
                continue;
            }
            father[x][y] = front;
            vis[x][y] = true;
            q.push((point) {x, y});
        }
    }
}

int main(){
    cin >> r >> c;
    for (int i = 1; i <= r; i++) {
        for (int j = 1; j <= c; j++) {
            cin >> a[i][j];
            if (a[i][j] == 'W') {
                s.x = i, s.y = j;
            }
        }
    }
    bfs();
}

T4 - WTX 的小车车

思路

这道题是解析几何的一个问题，首先我们看一下题，注意提示里面说了 WTX 的图纸只有一种可能。那么我们分析一下，一个三角形的重心与这个三角形的外接圆的圆心或者说外心相同，那么这个三角形是什么三角形呢？

首先我们了解一下三角形的重心是什么？根据百度百科的说法，三角形的重心是三角形三条中线的交点，我们可以举一个例子，如图-1，我们在平面直角坐标系 \(xOy\) 中作任意 \(\triangle ABC\) ，作 \(\triangle ABC\) 的三条中线 \(AD\) ，\(BE\)，\(CF\)，得到一个交点 \(G\) ，这个点就是我们的三角形的重心

图-1

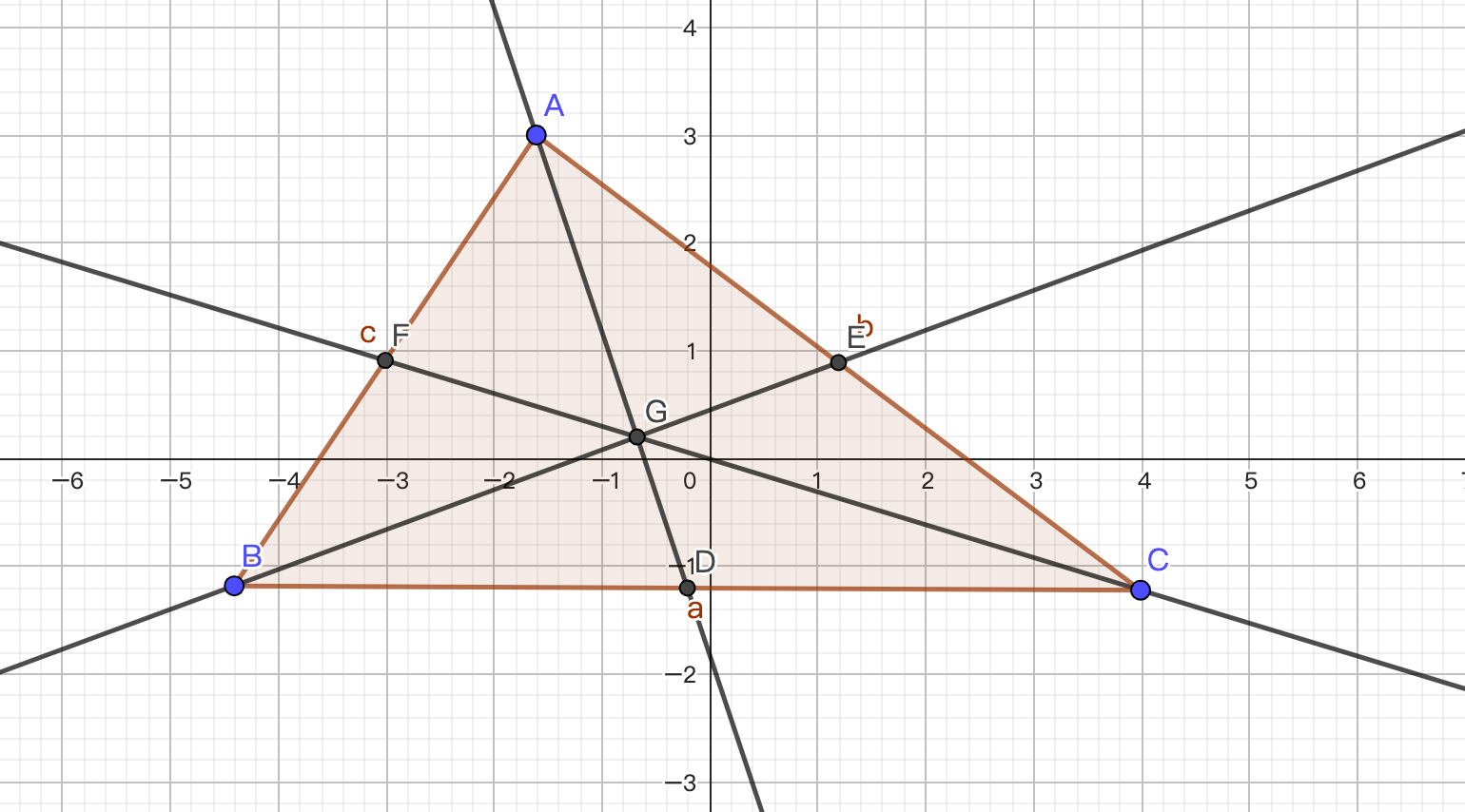
那么三角形的外接圆的圆心要怎么求呢，我们查阅教科书可以发现，三角形的外心就是三角形三条中垂线的交点，如图-2，图中的点 \(D\) 就是三角形的外心

图-2

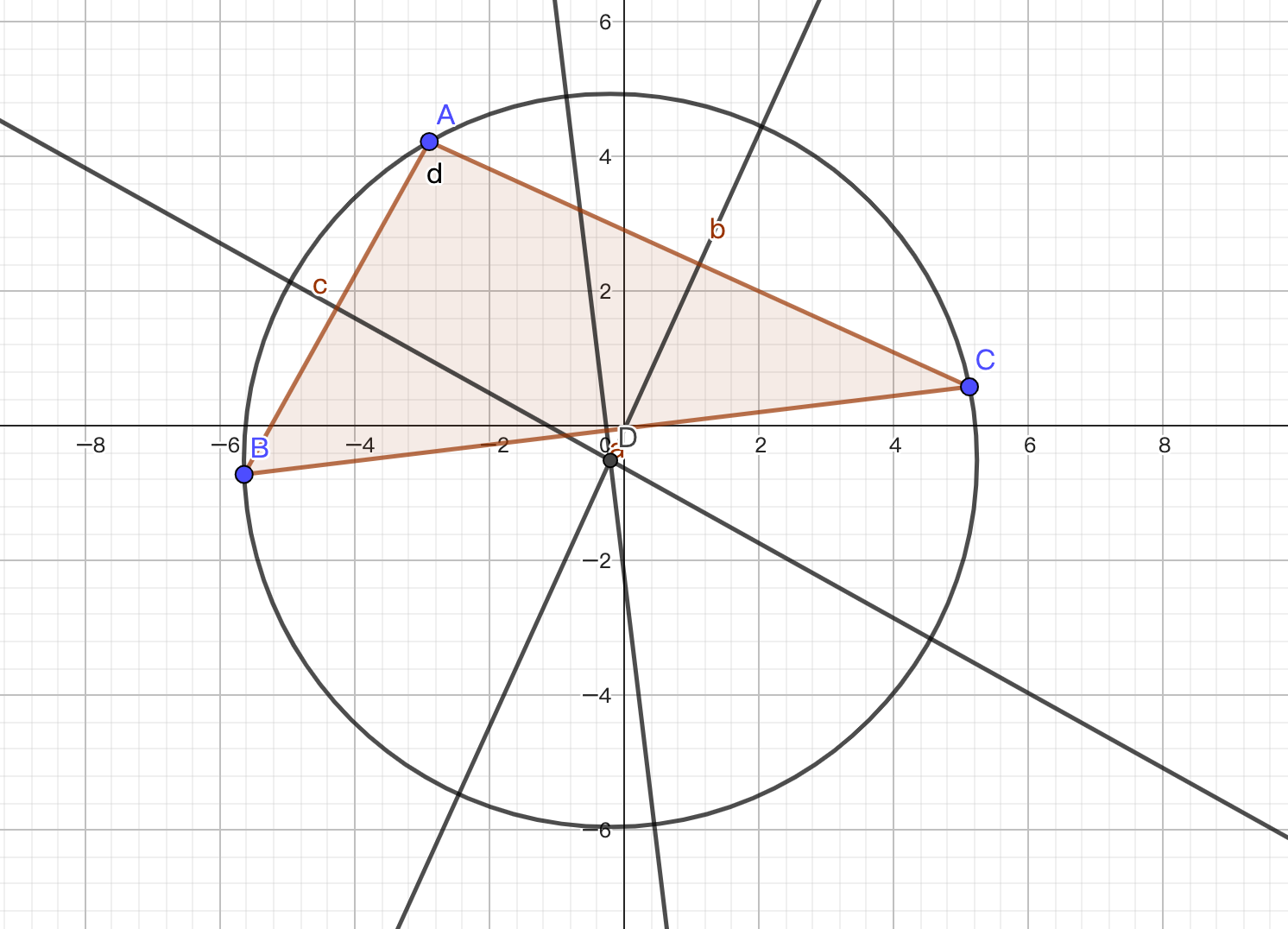
那么我们考虑在什么情况下中线的交点会和中垂线的交点重合？我们会发现，为了使中垂线与中线重合，三角形的中线必须要是三角形形的高线，也就是一边到对应点的垂线，那么符合这个标准的是什么三角形呢？我们想一想就会发现，只有正三角形可以满足这个要求。在正三角形中，三角形的三条中线是完全与中垂线重合的，那么这个时候三角形的重心就和外心就重合了，如图-3，点 \(G\) 就是三角形的重心兼外心

图-3

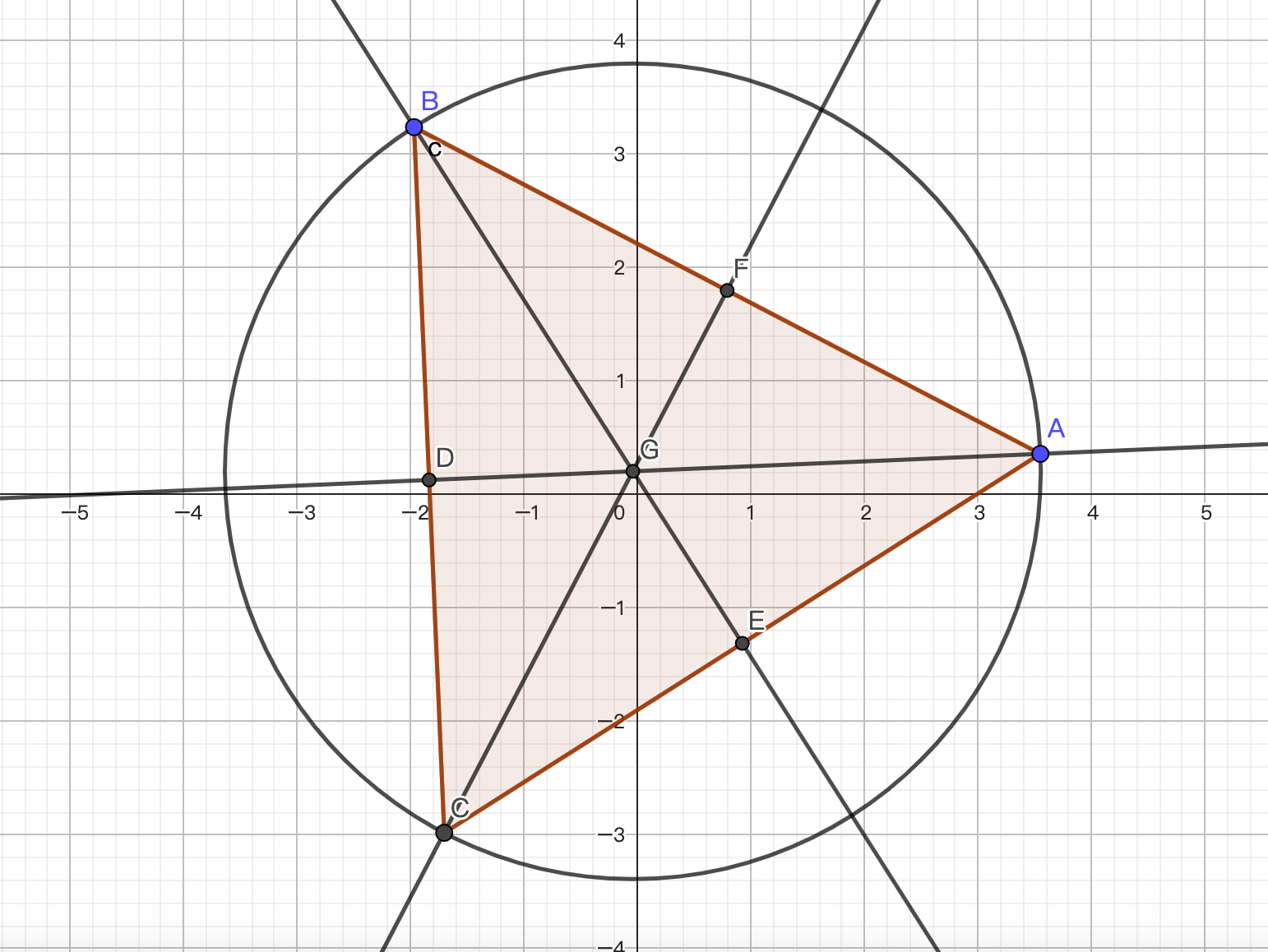
那么现在我们已经知道了 WTX 的图纸上面的框架是正三角形，那么我们要怎么统计这个正三角形的数量呢？讲到这里，不知道你有没有想起来一道经典的哈希表（散列表）题目 四轮车 呢？我们可以用一个哈希表来保存一些点，然后爆搜两个点，计算另一个点，然后统计数量，时间复杂度为 \(O(n ^ 2)\) 。是我力所能及的最优时间复杂度了，希望赛时能有巨佬写出更优秀的代码。

话说回来已知正三角形的两个顶点，怎么计算第三个顶点的坐标呢？

如图-4，首先作任意两点 \(A\) ，\(B\) 。连接 \(A\)，\(B\)，并分别以 \(A\)，\(B\) 为圆心，\(AB\) 为半径做两个圆，我们就会发现，两个圆相交的两个点 \(C\) 和 \(D\) 就是以 \(A\) 和 \(B\) 为两顶点可能的两个正三角形的顶点了

图-4

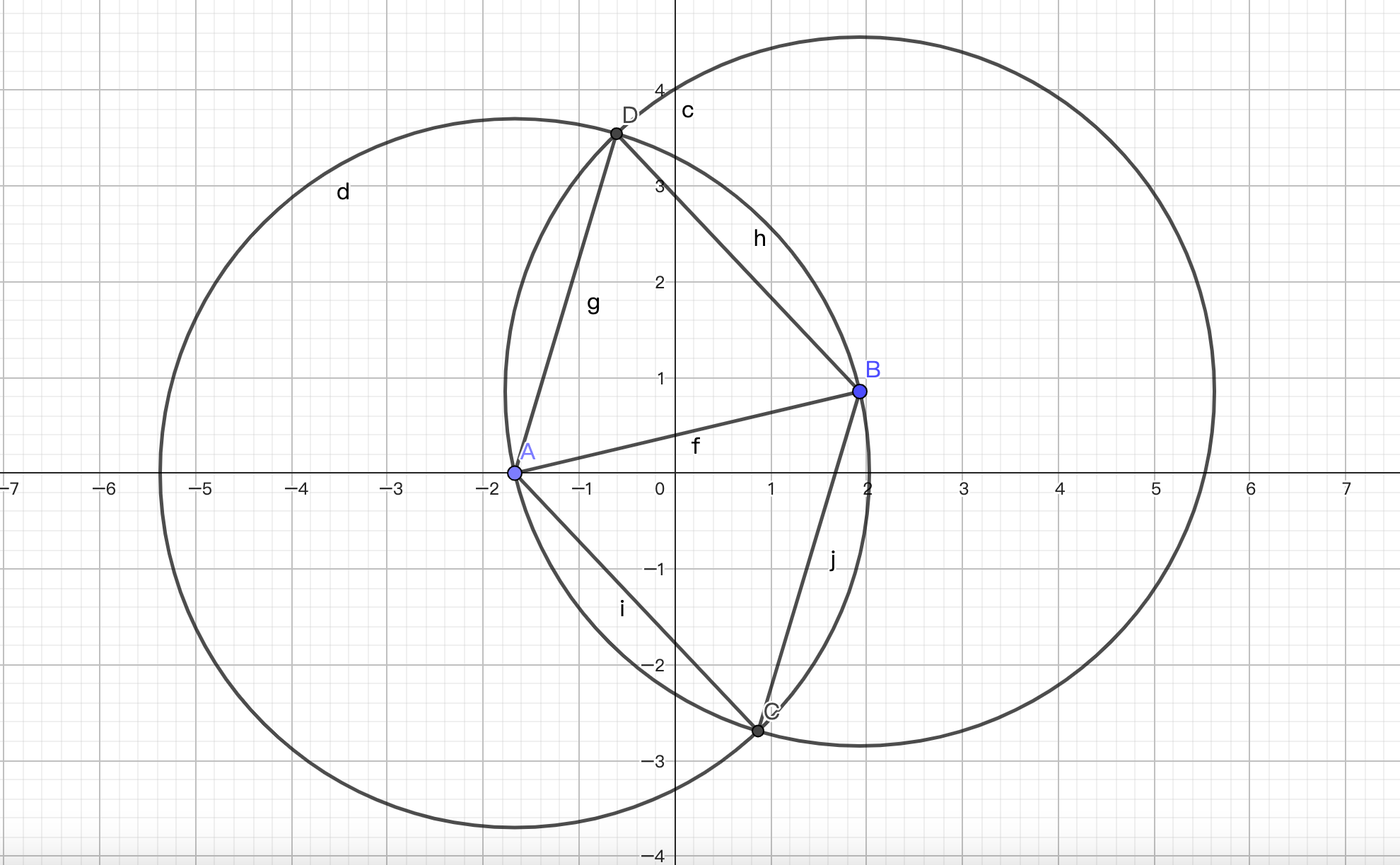
但是，我们要怎么求这两个圆的交点呢？我们首先复习一下高中数学选择性必修第一册 B 版第 103 页起的关于圆及其方程的内容。我们会发现，圆的方程是 \((x-a) ^ 2 + (y-b) ^ 2=r ^ 2\) ，那么我们可以尝试联立两个圆的方程，尝试求出这个二元二次方程组的两个根，但是我们稍微查阅一下相关资料就可以发现，对于这个二元二次方程组，我们通常会把他化简为一些更高次的方程，但是这些高次的方程由于没有通用的求根公式，所以求起来会十分的难受。综上所述，这个方法是很复杂的，我们需要寻求一个更加简便的方法。不过，我们也可以尝试用这种方法，看看究竟行不行。

下面提供几种思路，各位也可以使用其他高级的方法解决这个问题。

求坐标思路一

我们会发现，正三角形的顶点是其对边的垂线（或者中垂线）上的一点。那么这一点到他对边的距离是多少呢，我们做一个图就可以看出来，如图-5，已知图中的 线段 \(AB\)，如何求线段 \(CD\) 的长度呢？很显然，由于图中的 \(\angle \alpha = 90\degree\) 或者说 \(CD \bot AB\) 我们可以很方便的使用勾股定理来解决这个问题，我们首先根据勾股定理列出一条方程 \(|AD| ^ 2 + |CD| ^ 2=|AC| ^ 2\) ，由于 \(AC=AB=BC\) 且 \(D\) 是 \(AB\) 的二等分点（终点） 所以我们可以将方程化简为这种形式 \(\left(\frac{1}{2}|AB|\right) ^ 2 + |CD| ^ 2= |AB| ^ 2\) 那么现在我们将方程稍加化简整理，得到 \(|CD| = \sqrt{\frac{5}{4} \cdot |AB| ^ 2}\) 。好的，现在我们已经获得了线段 \(CD\) 的长度了，那么我们要怎么得到 直线 \(CD\) 的方程（解析式）呢？

图-5

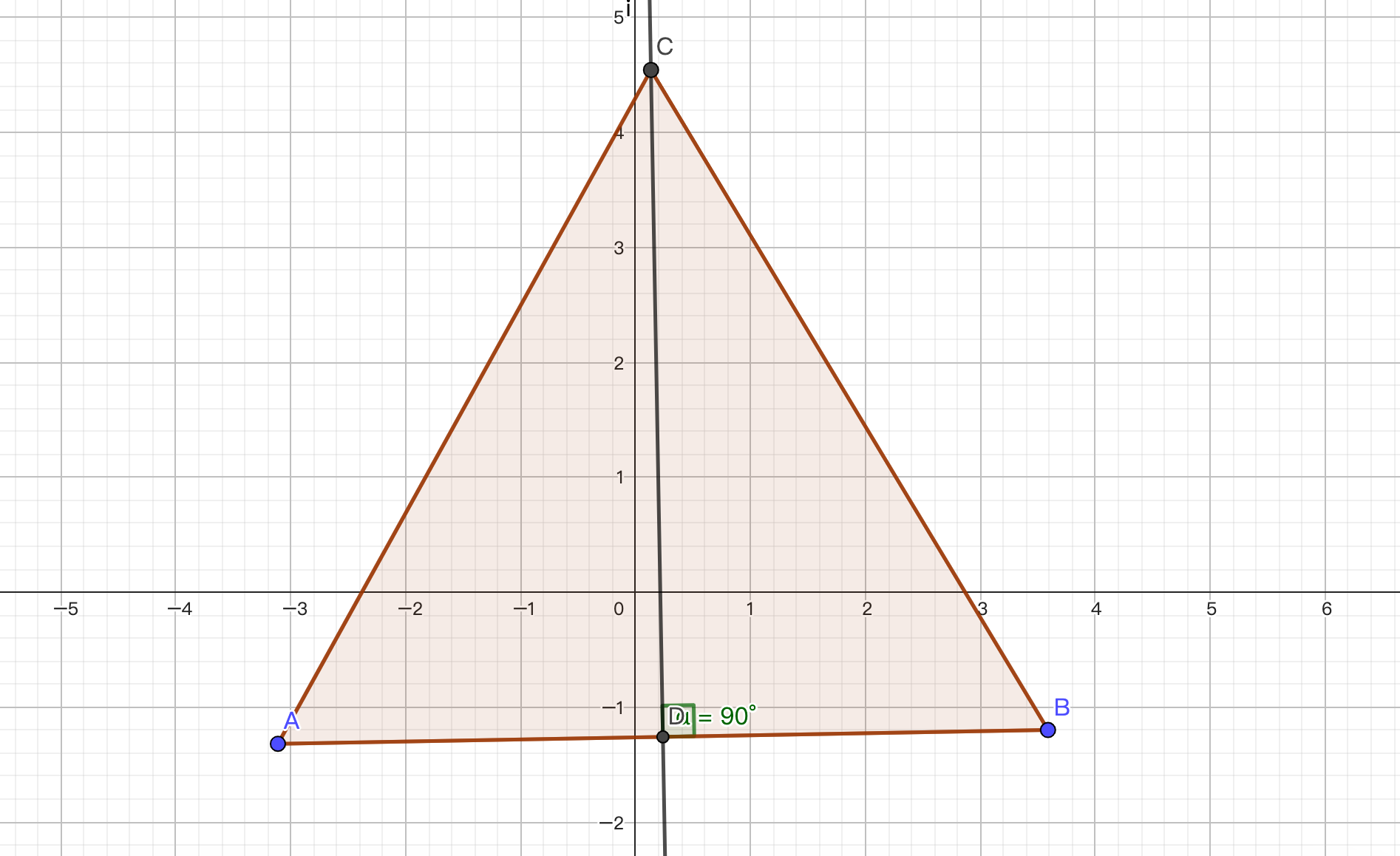
首先我们复习一下高中数学选择性必修第一册 B 版第 79 页起关于直线及其方程的内容。我们可以得知，表达一条直线有很多种方式，比如点斜式方程（\(y - y_0 = k\cdot(x - x_0)\)）、斜截式方程（\(y = kx + b\)）、两点式方程（\(\frac{y - y_1}{y_2 - y_1} = \frac{x - x_1}{x_2 - x_1}\)）等等…… 很显然，在我们的这道题目中，需要使用点斜式方程，因为直线 \(CD\) 的斜率以及点 \(D\) 的坐标是极其好求的，所以这种方法会比较简便。

首先我们解决一个比较简单的问题，点 \(D\) 的坐标要怎么求？由于点 \(D\) 是线段 \(AB\) 的中点，所以我们可以很方便的使用中点公式 \((\frac{x_2 - x_1}{2}, \frac{y_2 - y_1}{2})\) ，那么这里我们假设 \(A:(x_1, y_1)\)， \(B:(x_2, y_2)\)，带入公式可得 \(D:(\frac{x_2 - x_1}{2}, \frac{y_2-y_1}{2})\) 。

然后是斜率的问题，我们根据垂线的性质可以得到假设现在有两条直线，他们的斜率分别是 \(k_1\) 和 \(k_2\) ，如果两直线垂直，那么 \(k_1 \cdot k_2=-1\) ，或者说 \(k_1 = -\frac{1}{k_2}\) ，也就是说两直线垂直，斜率互为负倒数。既然如此，那么 \(CD\) 的斜率是否可求了呢？没错，首先我们假设 \(AB\) 的斜率为 \(k\)，且 \(A:(x_1, y_1)\)， \(B:(x_2, y_2)\)，由于 \(A\) 和 \(B\) 两点的坐标已知，那么我们很容易通过直线的斜截式方程得到 \(k = \frac{y_2 - y_1}{x_2 - x_1}\)，那么 \(CD\) 的斜率 \(k_1\) 就应当等于 \(\frac{y2-y_1}{x_2 - x_1}\) 的负倒数 \(-\frac{x_2 - x_1}{y_2 - y_1}\) 。

既然两个问题都解决了，那么我们假设 \(D:(x_3, y_3)\) ，将计算出来的结果带入直线的点斜式方程 \(y - y_0 = k \cdot (x - x_0)\) 中，我们可以得到 \(y - y_3 = -\frac{x_2 - x_1}{y_2 - y_1}\cdot (x - x_3)\) ，将点 \(D\) 的坐标代入方程可得 \(y - \frac{y_2 - y_1}{2} = -\frac{x_2 - x_1}{y_2 - y_1}\cdot (x - \frac{x_2 - x_1}{2})\) 。那么，是时候公布正确答案了，这条方程就是大名鼎鼎的中垂线方程！！！

现在一个问题又出现了，已知一条直线和一个点和一个距离，如何求直线上的另一点的坐标？

我这边的思路是这样子的，如图-6，我们会发现，如果我们以这个距离为半径，已知点为圆心，可以做出一个圆，而这个圆与我们的直线的交点就是我们想要求的两个点。

那么怎么求一个圆与直线的交点呢？下面介绍两种方法，方程法和向量法

方程法

方程法顾名思义，就是通过解方程来得到结果，首先我们要知道我们使用什么方程来计算，那么我们首先确认圆的方程，这里为了方便使用圆标准方程 \((x - a) ^ 2 + (y - b) ^ 2 = r ^ 2\) 。然后是较难确定的直线的方程，难确定的原因主要是直线的方程实在是太多种多样了，就课本里面的就有整整五种！我们这里选的直线的一般式方程 \(ax + by + c = 0\) ，需要注意的是，圆的方程中的常数 \(a\) 和 \(b\) 与直线方程内的常数 \(a\) 和 \(b\) 在大多数情况下是不会相等的，因此为了方便，我们将其加上下标后联立，得到一个这样的方程组：

\[ \left\{ \begin{array}{l} a_1x+b_1y+c = 0\ \\ (x - a_2)^2 + (y - b_2) ^ 2 = r ^ 2\ \end{array} \right. \]

解得

1
2
3
4
5
6
7
8
9
10
11
12
x =

- c - (b1*(b2 - a2*b1 - b1*c + (- a2 ^ 2 - 2*a2*b1*b2 - 2*a2*c - b1 ^ 2*b2 ^ 2 + b1 ^ 2*r ^ 2 - 2*b1*b2*c - c ^ 2 + r ^ 2) ^ (1/2)))/(b1 ^ 2 + 1)

  (b1*(a2*b1 - b2 + b1*c + (- a2 ^ 2 - 2*a2*b1*b2 - 2*a2*c - b1 ^ 2*b2 ^ 2 + b1 ^ 2*r ^ 2 - 2*b1*b2*c - c ^ 2 + r ^ 2) ^ (1/2)))/(b1 ^ 2 + 1) - c


y =

 (b2 - a2*b1 - b1*c + (- a2 ^ 2 - 2*a2*b1*b2 - 2*a2*c - b1 ^ 2*b2 ^ 2 + b1 ^ 2*r ^ 2 - 2*b1*b2*c - c ^ 2 + r ^ 2) ^ (1/2))/(b1 ^ 2 + 1)

-(a2*b1 - b2 + b1*c + (- a2 ^ 2 - 2*a2*b1*b2 - 2*a2*c - b1 ^ 2*b2 ^ 2 + b1 ^ 2*r ^ 2 - 2*b1*b2*c - c ^ 2 + r ^ 2) ^ (1/2))/(b1 ^ 2 + 1)

稍微整理一下得

\[ \left\{ \begin{array}{l} x=\left(\begin {array} { c } -c-\frac { b _ { 1 } \left(b _ { 2 } - a _ { 2 } b_{1} -b _ { 1 } c + \sqrt{ -{ a_{ 2 } } ^ 2-2a_{ 2 } b_{ 1 } b_{ 2 } -2a_{2} c- { b_{ 1 } } ^ 2 { b _ { 2 } } ^ 2+{b_{1 } } ^ 2r ^ 2-2b_{ 1 } b_{ 2 } c-c ^ 2+r ^ 2} \right) }{ {b_{1} } ^ 2+1}\\ \frac{b_{1}\left(a_{2}b_{1}-b_{2}+b_{1}c+\sqrt{-{a_{2}} ^ 2-2a_{2} b_{1} b_{2} -2a_{2} c-{b_{1}} ^ 2{b_{2}} ^ 2+{b_{1}} ^ 2r ^ 2-2b_{1} b_{2} c-c ^ 2+r ^ 2} \right) }{ {b_{1} } ^ 2+1} -c \end{array} \right )\\ y = \left(\begin{array}{c} \frac{b_{2} -a_{2} b_{1} -b_{1}c+\sqrt{-{a_{2}} ^ 2-2a_{2}b_{1}b_{2}-2a_{2}c-{b_{1}} ^ 2{b_{2}} ^ 2+{b_{1}} ^ 2r ^ 2-2b_{1}b_{2}c-c ^ 2+r ^ 2}}{ {b_{1} } ^ 2+1}\\ -\frac{a_{2}b_{1}-b_{2}+b_{1}c+\sqrt{-{a_{2}} ^ 2-2a_{2}b_{1}b_{2}-2a_{2}c-{b_{1}} ^ 2{b_{2}} ^ 2+{b_{1}} ^ 2r ^ 2-2b_{1}b_{2}c-c ^ 2+r ^ 2}}{ {b_{1} } ^ 2+1} \end{array}\right) \end{array} \right. \]

至于我是怎么解出来的吧，肯定不是手解的，毕竟这么长的式子，我的草稿纸都写不下，你说要怎么算出来这样的式子。这里需要借用一个工具：MatLab 打开网站后，你需要注册一个账户，然后就会有每个星期 \(20\) 个小时时间在线使用 MatLab 软件，软件的使用方法类似 Python Shell。

打开后，你会见到一个控制台，我们首先定义变量

1
syms a1 b1 a2 b2 c r x y

接着输入我们的方程组

1
f = [a1 * x + b1 * y + c == 0, (x - a2)  ^  2 + (y - b2)  ^  2 == r  ^  2]

然后求解

1
solve(f, [x, y])

之后你会得到一个变量 ans ，你需要从这个结构体中获得 \(x\) 和 \(y\) 的解，注意不能输入 ans.x 直接输出，这样会把 \(y\) 的解覆盖掉，我也不知道为什么。

你需要使用两个变量，比如 xans 和 yans 来转存结构体里面的数据，代码如下

1
2
xans = ans.x
yans = ans.y

然后你可以输入 xans 或者 yans 查看 \(x\) 的解或者 \(y\) 的解，或者你也可以输入 latex(xans) 或者 latex(yans) 将 \(x\) 的解或者 \(y\) 的解转化为优雅的 \(\LaTeX\) 代码

向量法

向量法比较巧妙，但是我看不懂，想学习的同学可以去看一下这一篇文章

求坐标思路二

我们写出两个圆的标准方程，并将其联立，尝试使用 MatLab 对其求根

\[ \left\{ \begin{array}{l} (x - a_1) ^ 2 + (y - b_1) ^ 2 = r ^ 2\\ (x - a_2) ^ 2 + (y - b_2) ^ 2 = r ^ 2 \end{array} \right. \]

我们求得的根如下

1
2
3
4
5
6
7
8
9
10
11
12
xans =

-(2*b1*(b1/2 + b2/2 - (a1*(-(a1 ^ 2 - 2*a1*a2 + a2 ^ 2 + b1 ^ 2 - 2*b1*b2 + b2 ^ 2 - 4*r ^ 2)/(a1 ^ 2 - 2*a1*a2 + a2 ^ 2 + b1 ^ 2 - 2*b1*b2 + b2 ^ 2)) ^ (1/2))/2 + (a2*(-(a1 ^ 2 - 2*a1*a2 + a2 ^ 2 + b1 ^ 2 - 2*b1*b2 + b2 ^ 2 - 4*r ^ 2)/(a1 ^ 2 - 2*a1*a2 + a2 ^ 2 + b1 ^ 2 - 2*b1*b2 + b2 ^ 2)) ^ (1/2))/2) - 2*b2*(b1/2 + b2/2 - (a1*(-(a1 ^ 2 - 2*a1*a2 + a2 ^ 2 + b1 ^ 2 - 2*b1*b2 + b2 ^ 2 - 4*r ^ 2)/(a1 ^ 2 - 2*a1*a2 + a2 ^ 2 + b1 ^ 2 - 2*b1*b2 + b2 ^ 2)) ^ (1/2))/2 + (a2*(-(a1 ^ 2 - 2*a1*a2 + a2 ^ 2 + b1 ^ 2 - 2*b1*b2 + b2 ^ 2 - 4*r ^ 2)/(a1 ^ 2 - 2*a1*a2 + a2 ^ 2 + b1 ^ 2 - 2*b1*b2 + b2 ^ 2)) ^ (1/2))/2) - a1 ^ 2 + a2 ^ 2 - b1 ^ 2 + b2 ^ 2)/(2*a1 - 2*a2)

-(2*b1*(b1/2 + b2/2 + (a1*(-(a1 ^ 2 - 2*a1*a2 + a2 ^ 2 + b1 ^ 2 - 2*b1*b2 + b2 ^ 2 - 4*r ^ 2)/(a1 ^ 2 - 2*a1*a2 + a2 ^ 2 + b1 ^ 2 - 2*b1*b2 + b2 ^ 2)) ^ (1/2))/2 - (a2*(-(a1 ^ 2 - 2*a1*a2 + a2 ^ 2 + b1 ^ 2 - 2*b1*b2 + b2 ^ 2 - 4*r ^ 2)/(a1 ^ 2 - 2*a1*a2 + a2 ^ 2 + b1 ^ 2 - 2*b1*b2 + b2 ^ 2)) ^ (1/2))/2) - 2*b2*(b1/2 + b2/2 + (a1*(-(a1 ^ 2 - 2*a1*a2 + a2 ^ 2 + b1 ^ 2 - 2*b1*b2 + b2 ^ 2 - 4*r ^ 2)/(a1 ^ 2 - 2*a1*a2 + a2 ^ 2 + b1 ^ 2 - 2*b1*b2 + b2 ^ 2)) ^ (1/2))/2 - (a2*(-(a1 ^ 2 - 2*a1*a2 + a2 ^ 2 + b1 ^ 2 - 2*b1*b2 + b2 ^ 2 - 4*r ^ 2)/(a1 ^ 2 - 2*a1*a2 + a2 ^ 2 + b1 ^ 2 - 2*b1*b2 + b2 ^ 2)) ^ (1/2))/2) - a1 ^ 2 + a2 ^ 2 - b1 ^ 2 + b2 ^ 2)/(2*a1 - 2*a2)


yans =

b1/2 + b2/2 - (a1*(-(a1 ^ 2 - 2*a1*a2 + a2 ^ 2 + b1 ^ 2 - 2*b1*b2 + b2 ^ 2 - 4*r ^ 2)/(a1 ^ 2 - 2*a1*a2 + a2 ^ 2 + b1 ^ 2 - 2*b1*b2 + b2 ^ 2)) ^ (1/2))/2 + (a2*(-(a1 ^ 2 - 2*a1*a2 + a2 ^ 2 + b1 ^ 2 - 2*b1*b2 + b2 ^ 2 - 4*r ^ 2)/(a1 ^ 2 - 2*a1*a2 + a2 ^ 2 + b1 ^ 2 - 2*b1*b2 + b2 ^ 2)) ^ (1/2))/2

b1/2 + b2/2 + (a1*(-(a1 ^ 2 - 2*a1*a2 + a2 ^ 2 + b1 ^ 2 - 2*b1*b2 + b2 ^ 2 - 4*r ^ 2)/(a1 ^ 2 - 2*a1*a2 + a2 ^ 2 + b1 ^ 2 - 2*b1*b2 + b2 ^ 2)) ^ (1/2))/2 - (a2*(-(a1 ^ 2 - 2*a1*a2 + a2 ^ 2 + b1 ^ 2 - 2*b1*b2 + b2 ^ 2 - 4*r ^ 2)/(a1 ^ 2 - 2*a1*a2 + a2 ^ 2 + b1 ^ 2 - 2*b1*b2 + b2 ^ 2)) ^ (1/2))/2

简单整理后如下

\[ \left\{ \begin{array}{l} x = \left(\begin{array}{c} -\frac{2\,b_{1}\,\left(\frac{b_{1}}{2}+\frac{b_{2}}{2}-\frac{a_{1}\,\sqrt{-\frac{ {a_{1}}^2-2\,a_{1}\,a_{2}+{a_{2}}^2+{b_{1}}^2-2\,b_{1}\,b_{2}+{b_{2}}^2-4\,r^2}{ {a_{1}}^2-2\,a_{1}\,a_{2}+{a_{2}}^2+{b_{1}}^2-2\,b_{1}\,b_{2}+{b_{2}}^2}}}{2}+\frac{a_{2}\,\sqrt{-\frac{ {a_{1}}^2-2\,a_{1}\,a_{2}+{a_{2}}^2+{b_{1}}^2-2\,b_{1}\,b_{2}+{b_{2}}^2-4\,r^2}{ {a_{1}}^2-2\,a_{1}\,a_{2}+{a_{2}}^2+{b_{1}}^2-2\,b_{1}\,b_{2}+{b_{2}}^2}}}{2}\right)-2\,b_{2}\,\left(\frac{b_{1}}{2}+\frac{b_{2}}{2}-\frac{a_{1}\,\sqrt{-\frac{ {a_{1}}^2-2\,a_{1}\,a_{2}+{a_{2}}^2+{b_{1}}^2-2\,b_{1}\,b_{2}+{b_{2}}^2-4\,r^2}{ {a_{1}}^2-2\,a_{1}\,a_{2}+{a_{2}}^2+{b_{1}}^2-2\,b_{1}\,b_{2}+{b_{2}}^2}}}{2}+\frac{a_{2}\,\sqrt{-\frac{ {a_{1}}^2-2\,a_{1}\,a_{2}+{a_{2}}^2+{b_{1}}^2-2\,b_{1}\,b_{2}+{b_{2}}^2-4\,r^2}{ {a_{1}}^2-2\,a_{1}\,a_{2}+{a_{2}}^2+{b_{1}}^2-2\,b_{1}\,b_{2}+{b_{2}}^2}}}{2}\right)-{a_{1}}^2+{a_{2}}^2-{b_{1}}^2+{b_{2}}^2}{2\,a_{1}-2\,a_{2}}\\ -\frac{2\,b_{1}\,\left(\frac{b_{1}}{2}+\frac{b_{2}}{2}+\frac{a_{1}\,\sqrt{-\frac{ {a_{1}}^2-2\,a_{1}\,a_{2}+{a_{2}}^2+{b_{1}}^2-2\,b_{1}\,b_{2}+{b_{2}}^2-4\,r^2}{ {a_{1}}^2-2\,a_{1}\,a_{2}+{a_{2}}^2+{b_{1}}^2-2\,b_{1}\,b_{2}+{b_{2}}^2}}}{2}-\frac{a_{2}\,\sqrt{-\frac{ {a_{1}}^2-2\,a_{1}\,a_{2}+{a_{2}}^2+{b_{1}}^2-2\,b_{1}\,b_{2}+{b_{2}}^2-4\,r^2}{ {a_{1}}^2-2\,a_{1}\,a_{2}+{a_{2}}^2+{b_{1}}^2-2\,b_{1}\,b_{2}+{b_{2}}^2}}}{2}\right)-2\,b_{2}\,\left(\frac{b_{1}}{2}+\frac{b_{2}}{2}+\frac{a_{1}\,\sqrt{-\frac{ {a_{1}}^2-2\,a_{1}\,a_{2}+{a_{2}}^2+{b_{1}}^2-2\,b_{1}\,b_{2}+{b_{2}}^2-4\,r^2}{ {a_{1}}^2-2\,a_{1}\,a_{2}+{a_{2}}^2+{b_{1}}^2-2\,b_{1}\,b_{2}+{b_{2}}^2}}}{2}-\frac{a_{2}\,\sqrt{-\frac{ {a_{1}}^2-2\,a_{1}\,a_{2}+{a_{2}}^2+{b_{1}}^2-2\,b_{1}\,b_{2}+{b_{2}}^2-4\,r^2}{ {a_{1}}^2-2\,a_{1}\,a_{2}+{a_{2}}^2+{b_{1}}^2-2\,b_{1}\,b_{2}+{b_{2}}^2}}}{2}\right)-{a_{1}}^2+{a_{2}}^2-{b_{1}}^2+{b_{2}}^2}{2\,a_{1}-2\,a_{2}} \end{array}\right) \\ y = \left(\begin{array}{c} \frac{b_{1}}{2}+\frac{b_{2}}{2}-\frac{a_{1}\,\sqrt{-\frac{ {a_{1}}^2-2\,a_{1}\,a_{2}+{a_{2}}^2+{b_{1}}^2-2\,b_{1}\,b_{2}+{b_{2}}^2-4\,r^2}{ {a_{1}}^2-2\,a_{1}\,a_{2}+{a_{2}}^2+{b_{1}}^2-2\,b_{1}\,b_{2}+{b_{2}}^2}}}{2}+\frac{a_{2}\,\sqrt{-\frac{ {a_{1}}^2-2\,a_{1}\,a_{2}+{a_{2}}^2+{b_{1}}^2-2\,b_{1}\,b_{2}+{b_{2}}^2-4\,r^2}{ {a_{1}}^2-2\,a_{1}\,a_{2}+{a_{2}}^2+{b_{1}}^2-2\,b_{1}\,b_{2}+{b_{2}}^2}}}{2}\\ \frac{b_{1}}{2}+\frac{b_{2}}{2}+\frac{a_{1}\,\sqrt{-\frac{ {a_{1}}^2-2\,a_{1}\,a_{2}+{a_{2}}^2+{b_{1}}^2-2\,b_{1}\,b_{2}+{b_{2}}^2-4\,r^2}{ {a_{1}}^2-2\,a_{1}\,a_{2}+{a_{2}}^2+{b_{1}}^2-2\,b_{1}\,b_{2}+{b_{2}}^2}}}{2}-\frac{a_{2}\,\sqrt{-\frac{ {a_{1}}^2-2\,a_{1}\,a_{2}+{a_{2}}^2+{b_{1}}^2-2\,b_{1}\,b_{2}+{b_{2}}^2-4\,r^2}{ {a_{1}}^2-2\,a_{1}\,a_{2}+{a_{2}}^2+{b_{1}}^2-2\,b_{1}\,b_{2}+{b_{2}}^2}}}{2} \end{array}\right) \end{array} \right. \]

很显然，我们求出了结果，但，就这么长一条式子，着实有些头痛。

现在我们已经求得了坐标，我们就可以通过一个哈希表（散列表）来存储每一个节点，然后查询，累加，得到结果，最后输出注意答案需要除以 \(3\) 因为三角形有 \(3\) 个顶点，而我们的程序会重复的计算每个节点，因此会计算真实答案的三倍。

标程

我们的标程使用方法二进行计算，虽然式子很长，但是代码量稍微少一些，主要是出题人很懒，代码不长，就 \(222\) 行，老天保佑赛时有人 \(\color{green}{AC}\)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
#include <iostream>
#include <vector>
#include <cmath>

using namespace std;

struct point {
    double x, y;
};

struct node {
    double x1, y1, x2, y2;
};

int hashx(double x, double y) {
    return abs(int(x + y) % 1007);
}

node calc(point a, point b) {
    double a1 = a.x, b1 = a.y, a2 = b.x, b2 = b.y, r = sqrt((a1 - a2) * (a1 - a2) + (b1 - b2) * (b1 - b2));
    double x1, y1, x2, y2;
    x1 = -(2 * b1 * (b1 / 2 + b2 / 2 - (a1 * sqrt(-((a1 * a1) - 2 * a1 * a2 + (a2 * a2) + (b1 * b1) - 2 * b1 * b2 +
                                                    (b2 * b2) - 4 * (r * r)) /
                                                  ((a1 * a1) - 2 * a1 * a2 + (a2 * a2) + (b1 * b1) - 2 * b1 * b2 +
                                                   (b2 * b2)))) / 2 + (a2 * sqrt(-((a1 * a1) - 2 * a1 * a2 + (a2 * a2) +
                                                                                   (b1 * b1) - 2 * b1 * b2 + (b2 * b2) -
                                                                                   4 * (r * r)) /
                                                                                 ((a1 * a1) - 2 * a1 * a2 + (a2 * a2) +
                                                                                  (b1 * b1) - 2 * b1 * b2 +
                                                                                  (b2 * b2)))) / 2) - 2 * b2 *
                                                                                                      (b1 / 2 + b2 / 2 -
                                                                                                       (a1 *
                                                                                                        sqrt(-((a1 *
                                                                                                                a1) -
                                                                                                               2 * a1 *
                                                                                                               a2 +
                                                                                                               (a2 *
                                                                                                                a2) +
                                                                                                               (b1 *
                                                                                                                b1) -
                                                                                                               2 * b1 *
                                                                                                               b2 +
                                                                                                               (b2 *
                                                                                                                b2) -
                                                                                                               4 * (r *
                                                                                                                    r)) /
                                                                                                             ((a1 *
                                                                                                               a1) -
                                                                                                              2 * a1 *
                                                                                                              a2 + (a2 *
                                                                                                                    a2) +
                                                                                                              (b1 *
                                                                                                               b1) -
                                                                                                              2 * b1 *
                                                                                                              b2 + (b2 *
                                                                                                                    b2)))) /
                                                                                                       2 + (a2 *
                                                                                                            sqrt(-((a1 *
                                                                                                                    a1) -
                                                                                                                   2 *
                                                                                                                   a1 *
                                                                                                                   a2 +
                                                                                                                   (a2 *
                                                                                                                    a2) +
                                                                                                                   (b1 *
                                                                                                                    b1) -
                                                                                                                   2 *
                                                                                                                   b1 *
                                                                                                                   b2 +
                                                                                                                   (b2 *
                                                                                                                    b2) -
                                                                                                                   4 *
                                                                                                                   (r *
                                                                                                                    r)) /
                                                                                                                 ((a1 *
                                                                                                                   a1) -
                                                                                                                  2 *
                                                                                                                  a1 *
                                                                                                                  a2 +
                                                                                                                  (a2 *
                                                                                                                   a2) +
                                                                                                                  (b1 *
                                                                                                                   b1) -
                                                                                                                  2 *
                                                                                                                  b1 *
                                                                                                                  b2 +
                                                                                                                  (b2 *
                                                                                                                   b2)))) /
                                                                                                           2) -
           (a1 * a1) + (a2 * a2) - (b1 * b1) + (b2 * b2)) / (2 * a1 - 2 * a2);
    x2 = -(2 * b1 * (b1 / 2 + b2 / 2 + (a1 * sqrt(-((a1 * a1) - 2 * a1 * a2 + (a2 * a2) + (b1 * b1) - 2 * b1 * b2 +
                                                    (b2 * b2) - 4 * (r * r)) /
                                                  ((a1 * a1) - 2 * a1 * a2 + (a2 * a2) + (b1 * b1) - 2 * b1 * b2 +
                                                   (b2 * b2)))) / 2 - (a2 * sqrt(-((a1 * a1) - 2 * a1 * a2 + (a2 * a2) +
                                                                                   (b1 * b1) - 2 * b1 * b2 + (b2 * b2) -
                                                                                   4 * (r * r)) /
                                                                                 ((a1 * a1) - 2 * a1 * a2 + (a2 * a2) +
                                                                                  (b1 * b1) - 2 * b1 * b2 +
                                                                                  (b2 * b2)))) / 2) - 2 * b2 *
                                                                                                      (b1 / 2 + b2 / 2 +
                                                                                                       (a1 *
                                                                                                        sqrt(-((a1 *
                                                                                                                a1) -
                                                                                                               2 * a1 *
                                                                                                               a2 +
                                                                                                               (a2 *
                                                                                                                a2) +
                                                                                                               (b1 *
                                                                                                                b1) -
                                                                                                               2 * b1 *
                                                                                                               b2 +
                                                                                                               (b2 *
                                                                                                                b2) -
                                                                                                               4 * (r *
                                                                                                                    r)) /
                                                                                                             ((a1 *
                                                                                                               a1) -
                                                                                                              2 * a1 *
                                                                                                              a2 + (a2 *
                                                                                                                    a2) +
                                                                                                              (b1 *
                                                                                                               b1) -
                                                                                                              2 * b1 *
                                                                                                              b2 + (b2 *
                                                                                                                    b2)))) /
                                                                                                       2 - (a2 *
                                                                                                            sqrt(-((a1 *
                                                                                                                    a1) -
                                                                                                                   2 *
                                                                                                                   a1 *
                                                                                                                   a2 +
                                                                                                                   (a2 *
                                                                                                                    a2) +
                                                                                                                   (b1 *
                                                                                                                    b1) -
                                                                                                                   2 *
                                                                                                                   b1 *
                                                                                                                   b2 +
                                                                                                                   (b2 *
                                                                                                                    b2) -
                                                                                                                   4 *
                                                                                                                   (r *
                                                                                                                    r)) /
                                                                                                                 ((a1 *
                                                                                                                   a1) -
                                                                                                                  2 *
                                                                                                                  a1 *
                                                                                                                  a2 +
                                                                                                                  (a2 *
                                                                                                                   a2) +
                                                                                                                  (b1 *
                                                                                                                   b1) -
                                                                                                                  2 *
                                                                                                                  b1 *
                                                                                                                  b2 +
                                                                                                                  (b2 *
                                                                                                                   b2)))) /
                                                                                                           2) -
           (a1 * a1) + (a2 * a2) - (b1 * b1) + (b2 * b2)) / (2 * a1 - 2 * a2);
    y1 = b1 / 2 + b2 / 2 - (a1 * sqrt(-((a1 * a1) - 2 * a1 * a2 + (a2 * a2) + (b1 * b1) - 2 * b1 * b2 + (b2 * b2) -
                                        4 * (r * r)) /
                                      ((a1 * a1) - 2 * a1 * a2 + (a2 * a2) + (b1 * b1) - 2 * b1 * b2 + (b2 * b2)))) /
                           2 + (a2 * sqrt(-((a1 * a1) - 2 * a1 * a2 + (a2 * a2) + (b1 * b1) - 2 * b1 * b2 + (b2 * b2) -
                                            4 * (r * r)) /
                                          ((a1 * a1) - 2 * a1 * a2 + (a2 * a2) + (b1 * b1) - 2 * b1 * b2 +
                                           (b2 * b2)))) / 2;
    y2 = b1 / 2 + b2 / 2 + (a1 * sqrt(-((a1 * a1) - 2 * a1 * a2 + (a2 * a2) + (b1 * b1) - 2 * b1 * b2 + (b2 * b2) -
                                        4 * (r * r)) /
                                      ((a1 * a1) - 2 * a1 * a2 + (a2 * a2) + (b1 * b1) - 2 * b1 * b2 + (b2 * b2)))) /
                           2 - (a2 * sqrt(-((a1 * a1) - 2 * a1 * a2 + (a2 * a2) + (b1 * b1) - 2 * b1 * b2 + (b2 * b2) -
                                            4 * (r * r)) /
                                          ((a1 * a1) - 2 * a1 * a2 + (a2 * a2) + (b1 * b1) - 2 * b1 * b2 +
                                           (b2 * b2)))) / 2;
    return (node) {x1, y1, x2, y2};
}

int n;
vector<point> a;
vector<point> v[1009];

void add(double x, double y) {
    int hx = hashx(x, y);
    a.push_back((point) {x, y});
    v[hx].push_back((point) {x, y});
}

int find(double x, double y) {
    int hx = hashx(x, y);
    for (int i = 0; i < v[hx].size(); i++) {
        if (abs(abs(v[hx][i].x) - abs(x)) <= 0.03 && abs(abs(v[hx][i].y) - abs(y)) <= 0.03) {
            return 1;
        }
    }
    return 0;
}

double x, y;

int main() {
    cin >> n;
    for (int i = 1; i <= n; i++) {
        cin >> x >> y;
        add(x, y);
    }
    int ans = 0;
    for (int i = 0; i < a.size(); i++) {
        for (int j = 0; j < a.size(); j++) {
            if (abs(abs(a[i].x) - abs(a[j].x)) <= 0.03 && abs(abs(a[i].y) - abs(a[j].y)) <= 0.03) {
                continue;
            }
            node points = calc(a[i], a[j]);
            double x1 = points.x1, x2 = points.x2, y1 = points.y1, y2 = points.y2;
            ans += find(x1, y1) + find(x2, y2);
        }
    }
    cout << (ans / 6);
}

总结

总的来说这场比赛由于是我出的第一场公开赛，多少有一些瑕疵，不过我个人还是乐在其中的，不知各位看完题解感觉如何，反正我整篇题解写下来近万字还是非常流畅的。最后，感谢 MCOI 的全体工作人员以及站长对比赛的大力支持，\(\huge{此致敬礼}\) 。

题解 > MCOI
MCOI 2023年6月月赛题解
https://lixuannan.github.io/posts/5946.html
作者
CodingCow Lee
发布于
2023年6月8日
许可协议