这道题一看就是连通块
因为求连通块 DFS
最简单,所以我用 BFS
简单思路:
首先把外围的 0 给清除掉,然后统计数组里面还有多少个
0。
那么难点来了,究竟怎样能一次把外围所有的 0
给清除呢?记不记得我们在输入的时候一般都会从 [1][1]
开始输入,那么是不是从 [1][1] 到 [n][n]
都有值?没错,有脑子都知道有值,那么这个矩阵的四周是不是空出了一圈是没有值的,就像这样:
1
2
3
| \0 \0 \0
\0 值 \0
\0 \0 \0
|
那么我们如果将外围的所有部分当做一个连通块来求的话,我们就可以把被
* 包围的 0
以外的所有部分找到,那么如果我们把所有部分都标记成 *
然后再遍历一次数组,把所有的 0
的个数统计起来,输出,那么是不是就可以 AC
了,不好意思,你太天真了,如果我们将这样的思路直接模拟出代码,那么 bfs
函数应该是这样的:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| struct pos{
int x, y;
};
queue<pos> q;
void bfs(int x, int y){
q.push((pos){x, y});
while (!q.empty()){
pos k = q.front();
q.pop();
for (int i=0; i <= 3; i++){
if (c[k.x + xx[i]][k.y + yy[i]] != '*'){
q.push((pos){k.x + xx[i], k.y + yy[i]});
c[k.x + xx[i]][k.y + yy[i]] = '*';
}
}
}
}
|
如果就这样自信运行的话那么你就会发现他报错
EXC_BAD_ACCESS (code=2, address=0x10b999e28) (我用 LLDB
看的)为什么呢?
如果我们用 LLDB
检测两个下标的数值,就会发现我们的下标变成了负数(我也是服了),要怎么避免呢?我们可以引入一个
bool check(int x, int y)
函数,用来检查下标的有效性。函数如下:
1
2
3
4
5
6
| bool check(int x, int y){
if (x < 0 || y < 0 || x > a + 1 || y > b + 1 || c[x][y] == '*'){
return false;
}
return true;
}
|
你可能会好奇为什么要检查是否过大呢?实际上这样可以使得速度加快,减少
BFS 的块。
好的,那么坑都解决了,对吗?可能对吧,至少我遇到过的就这些,那么代码写出来是什么样子的呢?
就长这样:(都看到这里了,点个赞吧,球球了)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
| #include <iostream>
#include <queue>
using namespace std;
struct pos {
int x, y;
};
int a, b, cnt, xx[4] = {-1, 1, 0, 0}, yy[4] = {0, 0, -1, 1};
char c[520][520];
bool check(int x, int y) {
if (x < 0 || y < 0 || x > a + 1 || y > b + 1 || c[x][y] == '*') {
return false;
}
return true;
}
queue<pos> q;
void clear(int x, int y) {
q.push((pos) {x, y});
while (!q.empty()) {
pos k = q.front();
q.pop();
for (int i = 0; i <= 3; i++) {
if (check(k.x + xx[i], k.y + yy[i])) {
q.push((pos) {k.x + xx[i], k.y + yy[i]});
c[k.x + xx[i]][k.y + yy[i]] = '*';
}
}
}
}
int main() {
cin >> a >> b;
for (int i = 1; i <= a; i++) {
for (int j = 1; j <= b; j++) {
cin >> c[i][j];
}
}
clear(0, 0);
for (int i = 1; i <= a; i++) {
for (int j = 1; j <= b; j++) {
if (c[i][j] == '0') {
cnt += 1;
}
}
}
cout << cnt;
}
|
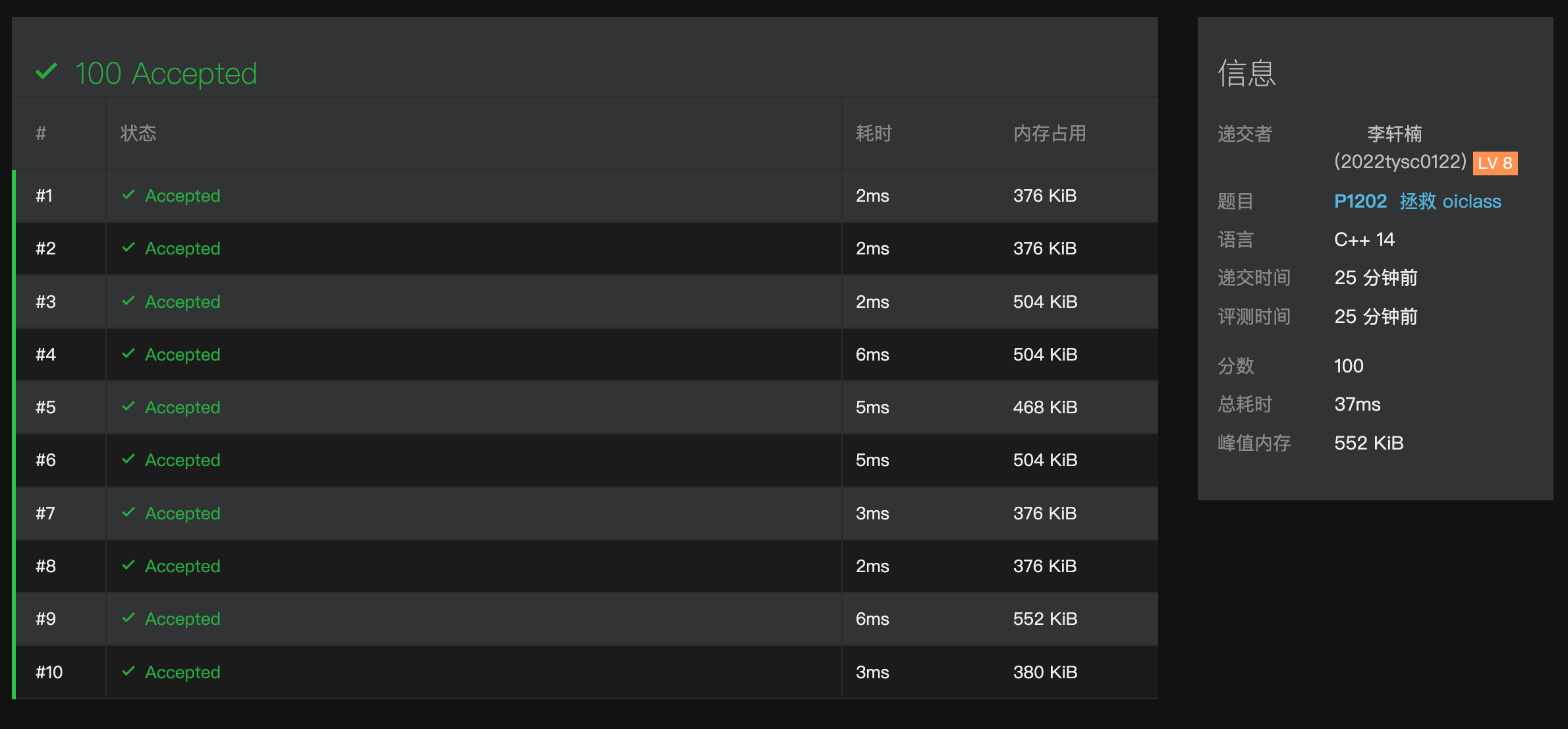 截屏2022-12-05 09.10.01
截屏2022-12-05 09.10.01
喜欢这篇文章?分享给你的朋友吧( ̄︶ ̄)↗


