OiClass PU2TI 330 Soso 的并查集题解

题意

Soso 欲将实现一个并查集，但是他写挂了。具体来说，他有 \(n\) 个点，第 \(i\) 个点的权值为 \(a_i\)，初始时每个点都是一棵有根树。

定义操作 \(find(x)\)，是找到 \(x\) 所在有根树的根。这次操作的代价是 \(x\) 到根的路径上所有点的点权和。

定义操作 \(merge(x,y)\)：

• 首先找到 \(x, y\) 所在有根树的根，记 \(x\prime=find(x), y\prime=find(y)\)。
• 若 \(x\prime \neq y\prime\)，将 \(y\prime\) 的父亲设为 \(x\prime\)。这意味着 \(x\prime\)、\(y\prime\) 这两棵有根树合并到一起，以后 \(find(x)\) 和 \(find(y)\) 应该相等。

明显，这个并查集的实现过程过于暴力，Soso 想计算一下它到底有多么暴力。给出 \(m\) 次 \(merge(x, y)\) 的操作，请求出所有操作中 \(find(x)\) 产生的代价总和，对 \(998244353\) 取模。

思路

观察到题目其实就是一个没有经过优化的并查集，要我们统计每一次合并的代价。很显然，这就是带权并查集，直接实现即可。参考 https://oi-wiki.org/ds/dsu/#带权并查集。但是带权并查集并不是一个很好写的东西，同时你可能不会，所以我们不用带权并查集。

注意到题目里面提到了“树”这个东西，于是我们考虑根据并查集合并的方式构建出一棵有根树。就是每一次 merge 的时候将 \(x\prime\) 和 \(y\prime\) 连边，然后暂时不统计答案。完全建好树之后，从根节点（就是 \(find(x)=x\) 的节点，自己想想为什么）进行一次 DFS，处理一个树上的前缀和。以样例为例，我们建树之后得到了下面的图：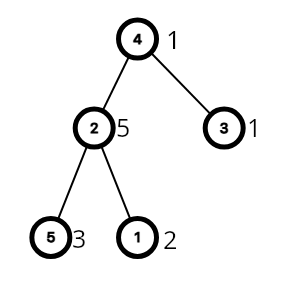

然后我们进行一次从上到下的前缀和，得到：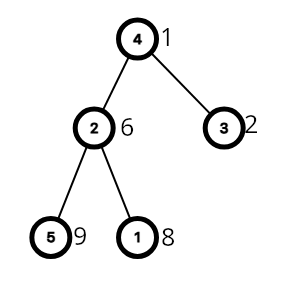

那么我们如何统计答案呢？不难发现，对于一次 \(find(x)\) 的代价，就是 \(s_{x} - s_{fa_{find(x)}}\)（其中 \(fa_i\) 意思是结点 \(i\) 的父结点，\(s\) 是前缀和数组）。这样，我们就实现了一个 \(O(n \alpha (n) + m)\) 的算法来维护这个东西。

代码

代码实现也很简单，在合并的时候拿个东西保存一下 \(find(x)\) 的值然后后面直接统计答案即可。注意由于取模的存在，可能会产生负数，因此要在取模的时候加上模数。

#include <iostream>
#include <vector>

#define int long long
#define mod 998244353

using namespace std;

int n, m, a[500009], u[500009], v[500009], fa[500009], f[500009];
vector<int> g[500009];
vector<pair<int, int>> queries;

int find(int x) {
    return x == fa[x] ? x : fa[x] = find(fa[x]);
}

void dfs(int u, int fa) {
    f[u] = fa;
    a[u] += a[fa];
    a[u] %= mod;
    for (int v: g[u]) {
        if (v != fa) {
            dfs(v, u);
        }
    }
}

signed main() {
    freopen("sosodsu.in", "rt", stdin);
    freopen("sosodsu.out", "wt", stdout);
    cin >> n >> m;
    for (int i = 1; i <= n; i++) {
        cin>> a[i];
        fa[i] = i;
    }
    for (int i = 1; i <= m; i++) {
        cin >> u[i] >> v[i];
        int uu = find(u[i]), vv = find(v[i]);
        queries.push_back({uu, u[i]});
        queries.push_back({vv, v[i]});
        if (uu != vv) {
            fa[vv] = uu;
            g[uu].push_back(vv);
            g[vv].push_back(uu);
        }
    }
    for (int i = 1; i <= n; i++) {
        if (find(i) == i) {
            dfs(i, 0);
        }
    }
    int ans = 0;
    for (auto &[x, y]: queries) {
        ans = ((ans - a[f[x]] + a[y]) % mod + mod) % mod;
    }
    cout << ans;
}