圆切线证明第二题题解

题目

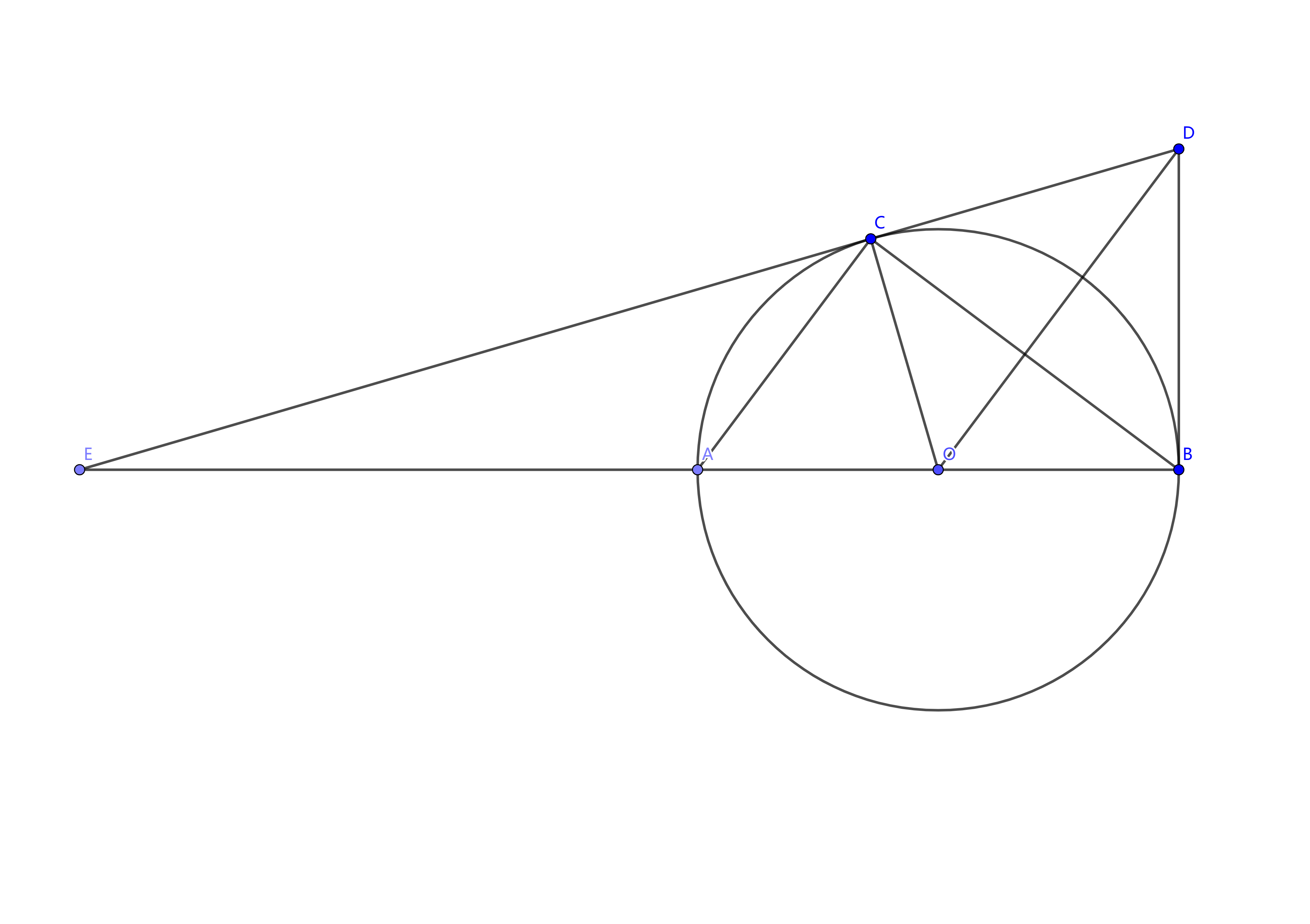
如图，\(AB\) 是 \(\odot O\) 的直径，\(CD\) 是 \(\odot O\) 的切线，\(C\) 为切点，\(BA\)、\(DC\) 的延长线交于点 \(E\)，连接 \(AC\)、\(OD\) 且 \(OD \parallel AC\)，连接 \(BD\).

(1) 求证：\(BD\) 是 \(\odot O\) 的切线； (2) 求 \(\frac{EC \cdot BD}{OB \cdot BE}\) 的值； (3) 若 \(AC=3\)，\(BC=4\)，求 \(ED\) 的长.

视频解析

思路

~~在 Geogebra 里面画出标准图然后直接得到答案。~~

第一问

题目要求我们证明切线，证明切线的一个常见的方法就是在确定有切点的情况下证明垂直。可以看到在题目中明确给出了 \(B\) 是圆上的一个点，于是我们满足了有切点的条件。

对于垂直，我们看到有 \(OD \parallel AC\)，因此可以得到 \(\angle {ACO} = \angle {COD}\) 且 \(\angle{CAO}=\angle{BOD}\). 又由 \(AO=CO\) 可得 \(\angle{ACO}=\angle{CAO}\). 综合起来可以得到 \(\angle{COD}=\angle{BOD}\). 不难发现，此时可以证明 \(\triangle{COD} \cong \triangle{BOD}\). 因为 \(CD\) 是 \(\odot O\) 的切线，所以我们可以得知 \(\angle{OCD}=90\degree\). 所以 \(\angle{OBD}=\angle{OCD}=90\degree\)，\(OB \perp BD\)。

综上，又因为 \(OB\) 是 \(\odot O\) 的半径，可以证明 \(BD\) 是 \(\odot O\) 的切线。

第二问

看到式子很容易联想到相似三角形，事实的确也是。

首先观察式子 \(\frac{EC \cdot BD}{OB \cdot BE}\) 中包含的四条线段，可以发现似乎他们很难构成一组相似三角形。但是由于 \(OB=OC\)，我们稍加转化就会发现一组相似三角形 \(\triangle{BED}\) 和 \(\triangle{CEO}\). 证明也不难，首先两个三角形有公共角 \(\angle{E}\)，还有切线所带来的两个直角 \(\angle{OCE}\) 和 \(\angle{DBE}\). 于是二者相似。

得到相似之后就有比例关系 \(\frac{OC}{DB}=\frac{CE}{BE}=\frac{EO}{ED}\)，选取前两组交叉相乘可以得到 \(OC \cdot BE = BD\cdot CE\). 又因为 \(OB=OC\)，因此 \(OB \cdot BE= EC \cdot BD\)，所以 \(\frac{EC \cdot BD}{OB \cdot BE} = 1\).

第三问

首先可以由勾股定理得到 \(AB=\sqrt[]{AC^2+BC^2}=5\)，于是半径就是 \(2.5\)。不难证明 \(\angle {ECA} = 90 \degree - \angle{ACO} = \angle{OCB} = \angle{OBC}\)，又因为 \(\angle{ E} = \angle{E}\)，所以 \(\triangle{AEC} \sim \triangle{CEB}\). 因此可以得到 \(\frac{CE}{BE} = \frac{AE}{CE} = \frac{AC}{BC} = \frac{3}{4}\).

由 \(\triangle{BED} \sim \triangle{CEO}\) 又可以得到 \(\frac{OC}{DB}=\frac{CE}{BE}=\frac{EO}{ED} = \frac{3}{4} = \frac{2.5}{DB}\). 不难算出 \(DB = \frac{10}{3}\).

同时我们可以得到 \(BE = AE + AB = AE + 5\)，\(CE = \frac{4}{3} AE\). 将其全部带入第二问中得到的 \(OB \cdot BE= EC \cdot BD\) 一式中可得 \(\frac{40}{9}AE = 2.5 \times(AE+5)\). 解得 \(AE = \frac{45}{7}\).

因此可得 \(CE = \frac{4}{3} AE = \frac{60}{7}\)，\(DE = CE + CD = CE + BD = \frac{250}{21}\)（由 \(\triangle{COD} \cong \triangle{BOD}\) 可得 \(CD = BD = \frac{10}{3}\)）。

“觉得不错的话，给点打赏吧 (✿◕‿◕✿)”