这是一道几何题
看到题目,我们会发现,题目需要我们找到四个点,构成一些正方形(即四边等长的矩形,这个很重要,后面会用到),然后输出可以构成的正方形的个数
好的,那么作为一个暴力骗分的小能手,我的第一反应就是暴力,简单估一下,如果有 \(n\) 个点,那么时间复杂度就是 \(O(n^4)\) 很明显,这个时间复杂度直接原地起飞了,能 AC 我直接把题目吃下去好吧
那么我们现在就要来考虑如何尽可能的减少枚举的点的数量,由于正方形只有四个顶点,那么我们考虑以下几种可能:
- 只有一个点,如图1,我们就可以看到,一个点可以确定无数个正方形,因此这种方法是不对滴!
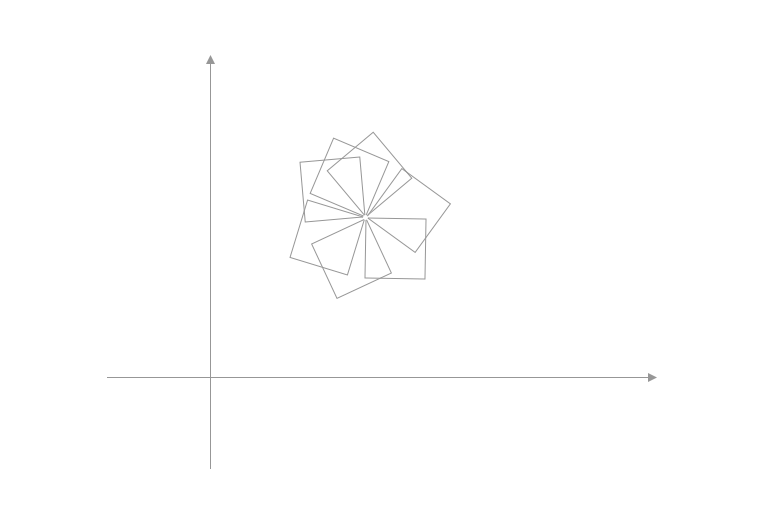
- 两个点,如图2,我们可以发现,只需要两个点,我们就可以完美的定位三个正方形,✌🏻
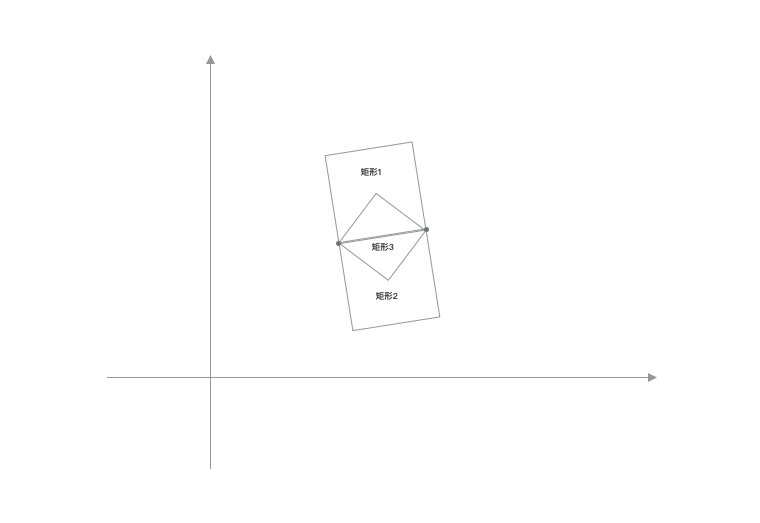
那我们要怎样通过已知的两个不重合的点获得另外两个点的坐标呢?首先我们需要一些前置的知识
如何判断三角形全等:根据极其聪明的 New Bing 的回答,判断三角形全等有五种方法:1、SSS(边边边):三边对应相等的三角形是全等三角形。2、SAS(边角边):两边及其夹角对应相等的三角形是全等三角形。3、ASA(角边角):两角及其夹边对应相等的三角形全等。4、AAS(角角边):两个内角和一条外接边分别对应相等的两个三角形全等。5、HL(斜直直):直角三角形中,斜边和一条直角边分别对应相等的两个三角形全等。我感觉还是比较准确的,OK,那么下一个
平面直角坐标系:从 New Bing 的口中可以得知:平面直角坐标系是一种用来表示平面内点的位置的方法。它由两条互相垂直且有公共原点的数轴组成,分别称为 \(x\) 轴和 \(y\) 轴。任何一个平面内的点都可以用一对有序数 \((x, y)\) 来表示,这就是它的坐标。此外,平面直角坐标系还有一些有用的性质:平面直角坐标系有一些基本的性质,例如:
坐标平面内的点与有序实数对一一对应
两个点的中点的坐标是它们的坐标的算术平均数
两个点之间的距离等于它们的横纵坐标差的平方和的开方
平行线具有相同或相反的斜率
如图3,我们构建一个平面直角坐标系,在坐标系上确认两点,分别定义为 点 \(A\) 和 点 \(B\) ,这两个点的坐标分别是 \((x1, y1)\) 和 \((x2, y2)\) .
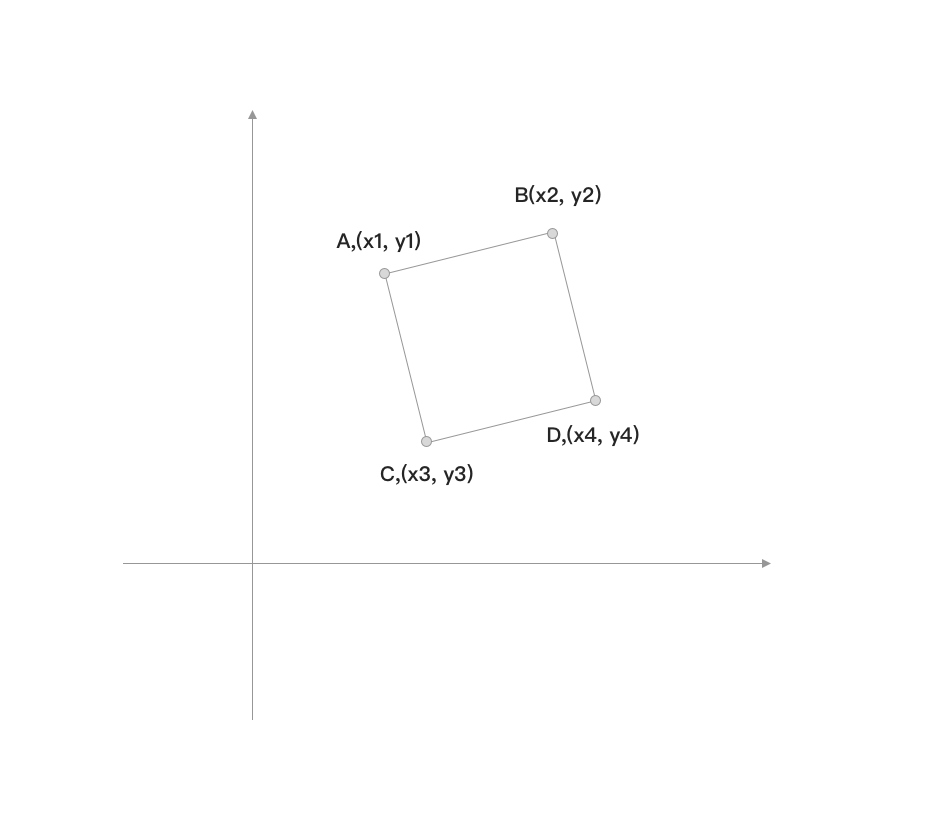
这时候,我们应该如何求出图片中 点 \(C\) 与 点 \(D\) 的坐标呢,我们可以过 点 \(A\) 做一条平行于 \(y\) 轴的直线,在过 点 \(C\) 做一条与 \(x\) 轴平行的直线,将两条直线的交点记为 点 \(E\),使得 \(\angle AEC=90 \degree\) ,同理,画出另外四面的角,如图4.
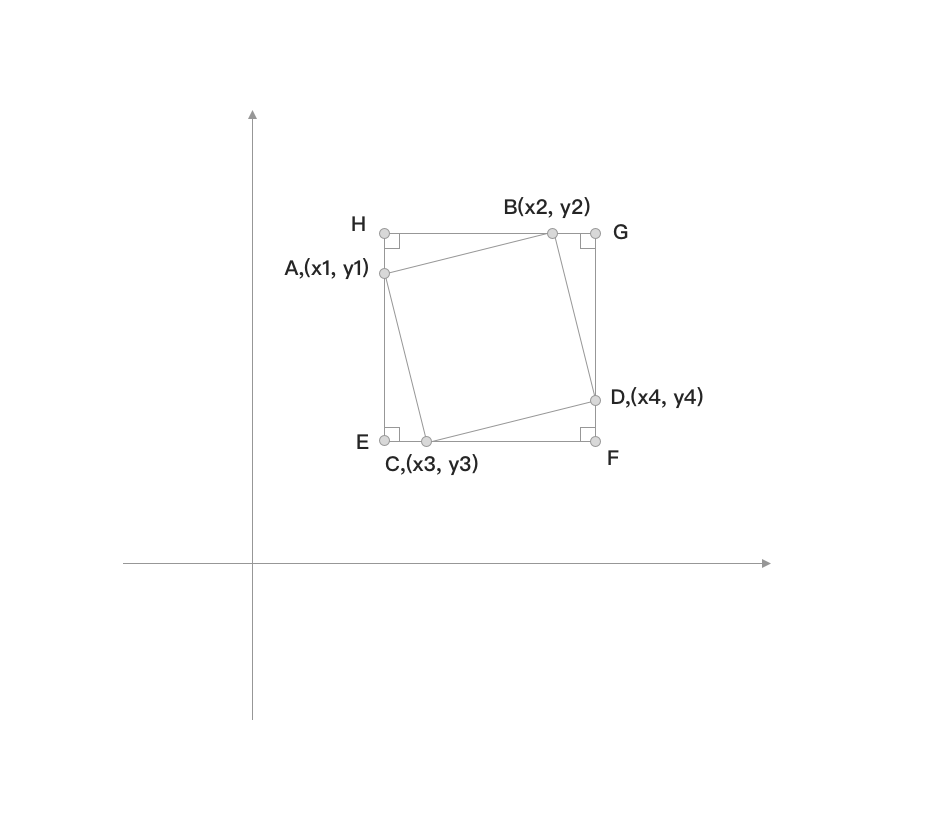
那么我们就可以发现,好像 \(AE=BH=FG=CD\) 且 \(AH=CE=DF=BG\)
,但是我们并没有证据,如果比赛的话我就直接打了,但是我们现在是正常做题,因此我们需要尝试证明一下这两条公式。观察可以发现,我们只需要证明
\(\triangle AEC\cong \triangle
CDF\cong\triangle BGF\cong\triangle AHB\)
,就可以证明以上的两个猜测,那么下面是严谨的证明步骤: $$
\begin{array}{lr} HAB + ABH=180 - AGH =180- BAC = 90\ 又 HAG +
EAC=180-BAC=90 \ HAB+EAC= HAB+ABH\ EAC=ABH\ AHB=AEC, EAC=ABH, AB=AC\ AEC
������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������用 New Bing (不知道为什么我的比起 Chrome
好像没什么特殊的功能)。你只需要在这个连接里面下载安装就可以了
2. 然后你需要安装一个浏览器插件:ModHeader
- Modify HTTP headers - Microsoft Edge Addons 3.
然后你需要把插件设置成这样: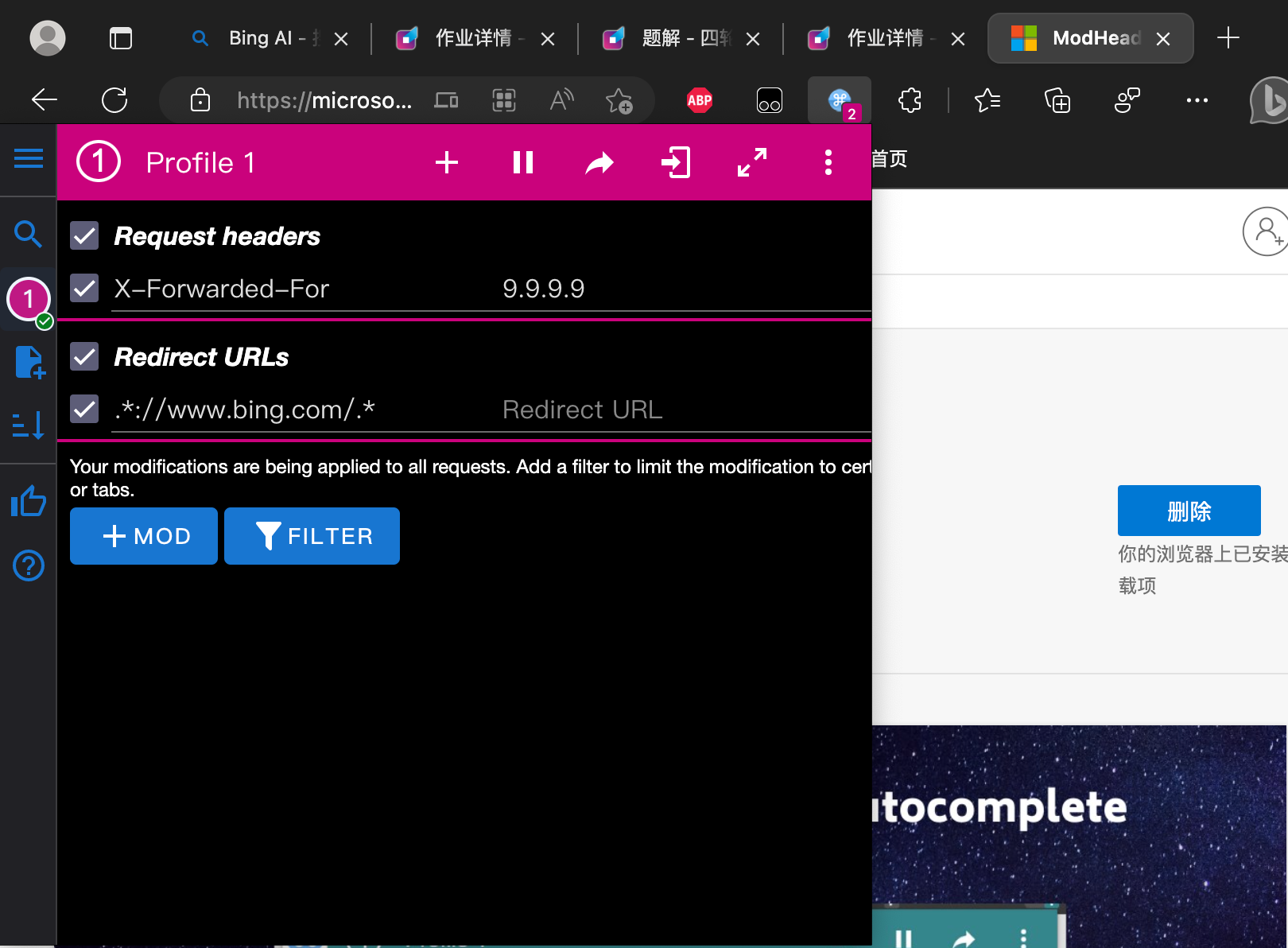
步骤的话实际上还好,首先把原本就有的 Request headers 栏里面填上"X-Forwarded-For" 和 "9.9.9.9",然后点击 "+ mod" -> "Redirect URL" 然后把 Redirect URL 栏里面填上 ".://www.bing.com/." 和 "(空)"
- 访问 www.bing.com/new 点击申请,直接加入候补名单,然后等待收到通过的邮件
- 收到邮件以后,打开 www.bing.com 然后点击左上角的 "聊天" ,就可以和世界上最聪明的 AI 玩耍啦啦啦
“觉得不错的话,给点打赏吧 (✿◕‿◕✿)”

微信支付

支付宝支付 (暂不支持)