CF1368E Ski Accidents 题解
思路
首先我们看到题中给出,这个图是一个
DAG,因此很容易的就可以想到拓扑排序。那么我们在思考一下,如何满足题目中给出的删除的点不超过
\(\frac{4}{7}n\)
的要求。我们可以举一个例子,看到下面的二叉树:
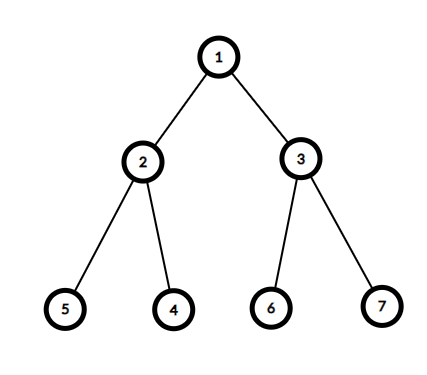
如果我们按照拓扑排序遍历,每次遍历到深度对 \(3\) 取模为 \(0\)
的节点,就删除。那么很显然,这个策略可以正常的分割出符合条件的链。同时,对于这个具有
\(7\) 个节点的图,他只删除了 \(4\) 个节点,满足题目 \(\frac{4}{7}n\) 的限制。
由此我们可以发现,无论怎么删除,都可以满足题目 \(\frac{4}{7}n\)
的限制。那么只要我们按照拓扑序遍历这个图,遇到深度超的就删除,就可以简单的水掉这一道紫题。
代码
拓扑序遍历即可,注意多测要清空。代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
| #include <iostream>
#include <vector>
#include <queue>
#include <algorithm>
using namespace std;
int n, m, u, v, d[200009], dp[200009];
vector<int> g[200009], ans, a[4];
int main() {
int t;
cin >> t;
while (t--) {
for (int i = 1; i <= n; i++) {
d[i] = 0;
dp[i] = 0;
g[i].clear();
}
ans.clear();
cin >> n >> m;
for (int i = 1; i <= m; i++) {
cin >> u >> v;
g[u].push_back(v);
d[v] += 1;
}
queue<int> q;
for (int i = 1; i <= n; i++) {
if (!d[i]) {
q.push(i);
dp[i] = 1;
}
}
while (!q.empty()) {
int u = q.front();
q.pop();
if (dp[u] >= 3) {
dp[u] = 0;
ans.push_back(u);
}
for (int v: g[u]) {
d[v] -= 1;
dp[v]= max(dp[v], dp[u] + 1);
if (!d[v]) {
d[v] = -1;
q.push(v);
}
}
}
cout << ans.size() << endl;
for (int i: ans) {
cout << i << " ";
}
}
}
|
喜欢这篇文章?分享给你的朋友吧( ̄︶ ̄)↗


