OiClass 2024 CSP-J 公益赛 #4 题解

引言

这场比赛出题人认为是 \(\approx\) CSP-J + 的难度，预估的平均分在 \(200\) 分左右。比赛的命题思路简单来说就是第一题水题但是考虑在题面里面写很多抽象的东西混淆视听；第二题有些思路的结论题，如果猜出了结论复杂度应该还是非常优秀的；第三题是本场比赛最难的题，算法本身并不难，但是这个思路上有一个优化很难想，这就给很多选手做题带来了很大的困扰，可能无人 AC；第四题是原题加强的版本，卡掉了原题的一种水法，是一道比较好想的 DP，代码上有两个坑，希望有人 AC；第五题纯粹出于兴趣，老天保佑有人 AC。

总而言之，这场比赛都是原题/原题的加强题目，具体对应关系如下：

  1. 好吧，T1 并不是原题。

  2. Codeforces Round 913 (Div. 3) C（CF1907C）改输入格式。

  3. COCI 2006 \(\sim\) 2007 #6 T4 KAMEN（洛谷 P6370）改输入格式。

  4. OiClass PUJI 域 C 班赛后康复训练赛 T3（OiClass PUJI 域 1348）改输入格式。

当然，所有题的题目背景和题目的描述都经过了巨大的改动，同时数据也都是有出题人亲手制造的。有需要者可以向出题人索要数据。

突破突破突破 (upgrade)

思路

不难发现，全部使用经验值最少的绿色经验书是最优秀的。因此我们直接计算 \(\lfloor \frac{x}{10} \rfloor\) 即可。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
#include <iostream>

#define int long long

using namespace std;

int x;

signed main() {
    freopen("upgrade.in", "rt", stdin);
    freopen("upgrade.out", "wt", stdout);
    cin >> x;
    cout << x / 10 << " " << 0 << " " << 0;
}

压缩名字 (compress)

思路

首先，这道题一眼看上去应该是可以用某种策略搞定的，但是由于策略太难想，并没有任何人采用这种方式（不过出题人猜测是因为这种方法时间复杂度不够优秀）。于是我们便看可以考虑如何统计出删除后的数字。我们从删除的策略入手，题目说删除相邻的两个不同的字符，实际上如果我们利用这个策略一直删，无论相隔多远，这要某一个字符能被删除，广义上来讲，就可以和任何另一个可删除的字符所相互配对。那么也就是说，我们把题目中给出的条件变为了删除任意两个不同的字符。然后我们考虑用这种策略删除后的情况。

  • 如果一个字母的出现次数 \(> \frac{1}{2} |s_i|\) （大于字符串长度的二分之一），那么此时这个字符串是无法被消除完的，即使所有的字符都用于消除这个特别多的字符，也会剩下一些。这个一些很容易计算，如果我们设字符串长度为 \(n\)，最多的字符数量为 \(m\)，那么就是 \(n - 2(n - m) = 2m - n\)。

  • 其余的情况，如果字符串长度是奇数，那么答案为 \(1\)，否则为 \(0\)。

简单实现即可，时间复杂度为 \(\mathcal{O}(n\cdot|s_i|) \leq 10^8\) 可以通过。但是由于题目的输入量非常大，简单的 cin / cout 是无法在如此的时间内完成输入的。同时又因为题目十分恶心的没有给出字符串的长度，因此我们必须使用 cin / cout 或者快读。那么 cin / cout 还能优化了吗？

cin / cout 优化

答案显然是可以的，我们首先可以关闭流输入输出（cin / cout，下同）与标准输入输出（printf/scanf，下同）的连接，使用代码 ios::sync_with_stdio(false)（无需额外头文件），然后我们解除流输入输出所绑定的函数，两行代码：cin.tie(nullptr) 和 cout.tie(nullptr)。这样我们的流输入输出便跑的比较快了。不过需要注意的是，关闭输入流同步后，不可以混用 cin / scanf 或 cout / printf，但是 cin / printf 和 scanf / cout 的组合仍然是可以使用的。

快读快写

快读快写是一种更进阶的方式，可以将输入输出的效率推到极致，但是编写不当导致 RE 的风险很高，慎用。这种方法效率高的原因主要是因为没有繁杂的处理，运用自定义的函数来达到极高的效率，下面给出一个可用的快读快写模板（调用 read(...) / write(...) 使用）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
#include <iostream>
#include <cstring>

#define endl '\n'

using namespace std;

inline void read(double &x) { scanf("%lf", &x); };

inline void write(double x) { printf("%lf", x); };

inline void read(long double &x) { scanf("%Lf", &x); };

inline void write(long double x) { printf("%Lf", x); };

template<typename type>
inline void read(type &x) {
    x = 0;
    bool flag(0);
    char ch = getchar();
    while (!isdigit(ch))flag ^= ch == '-', ch = getchar();
    while (isdigit(ch))x = (x << 1) + (x << 3) + (ch ^ 48), ch = getchar();
    flag ? x = -x : 0;
}

template<typename type>
inline void write(type x) {
    x < 0 ? x = -x, putchar('-') : 0;
    static short Stack[50], top(0);
    do Stack[++top] = x % 10, x /= 10; while (x);
    while (top)putchar(Stack[top--] | 48);
}

inline char read(char &ch) {
    char c = getchar();
    while (c == ' ' || c == '\n')c = getchar();
    return ch = c;
}

inline void read(char *x) {
    static char ch;
    read(ch);
    do *(x++) = ch; while (!isspace(ch = getchar()) && ~ch);
}

template<typename type>
inline void write(type *x) { while (*x)putchar(*(x++)); }

inline void read(std::string &x) {
    static char ch;
    read(ch), x.clear();
    do x += ch; while (!isspace(ch = getchar()) && ~ch);
}

inline void write(const std::string &x) { for (int i = 0, len = x.length(); i < len; ++i)putchar(x[i]); }

inline char write(const char &ch) { return putchar(ch); }

template<typename type, typename ...T>
inline void read(type &x, T &...y) { read(x), read(y...); }

template<typename type, typename ...T>
inline void write(type x, T...y) { write(x), write(y...); }

通过上面对输入输出的优化，我们就可以正常的 AC 了。

代码

简单优化版本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#include <iostream>
#include <cstring>

#define endl '\n'

using namespace std;

int n, a[30];
string s;

signed main() {
    freopen("compress.in", "rt", stdin);
    freopen("compress.out", "wt", stdout);
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);
    cin >> n;
    for (int i = 1; i <= n; i++) {
        cin >> s;
        memset(a, 0, sizeof(a));
        for (char j: s) {
            a[j - 'a'] += 1;
        }
        int x = 0;
        for (int j = 0; j < 26; j++) {
            x = max(x, a[j]);
        }
        cout << (x > (s.size() >> 1) ? (x << 1) - s.size() : s.size() & 1) << endl;
    }
}

快读快写版本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
#include <iostream>
#include <cstring>

#define endl '\n'

using namespace std;

inline void read(double &x) { scanf("%lf", &x); };

inline void write(double x) { printf("%lf", x); };

inline void read(long double &x) { scanf("%Lf", &x); };

inline void write(long double x) { printf("%Lf", x); };

template<typename type>
inline void read(type &x) {
    x = 0;
    bool flag(0);
    char ch = getchar();
    while (!isdigit(ch))flag ^= ch == '-', ch = getchar();
    while (isdigit(ch))x = (x << 1) + (x << 3) + (ch ^ 48), ch = getchar();
    flag ? x = -x : 0;
}

template<typename type>
inline void write(type x) {
    x < 0 ? x = -x, putchar('-') : 0;
    static short Stack[50], top(0);
    do Stack[++top] = x % 10, x /= 10; while (x);
    while (top)putchar(Stack[top--] | 48);
}

inline char read(char &ch) {
    char c = getchar();
    while (c == ' ' || c == '\n')c = getchar();
    return ch = c;
}

inline void read(char *x) {
    static char ch;
    read(ch);
    do *(x++) = ch; while (!isspace(ch = getchar()) && ~ch);
}

template<typename type>
inline void write(type *x) { while (*x)putchar(*(x++)); }

inline void read(std::string &x) {
    static char ch;
    read(ch), x.clear();
    do x += ch; while (!isspace(ch = getchar()) && ~ch);
}

inline void write(const std::string &x) { for (int i = 0, len = x.length(); i < len; ++i)putchar(x[i]); }

inline char write(const char &ch) { return putchar(ch); }

template<typename type, typename ...T>
inline void read(type &x, T &...y) { read(x), read(y...); }

template<typename type, typename ...T>
inline void write(type x, T...y) { write(x), write(y...); }

int n, a[30];
string s;

signed main() {
    freopen("compress.in", "rt", stdin);
    freopen("compress.out", "wt", stdout);
    read(n);
    for (int i = 1; i <= n; i++) {
        read(s);
        memset(a, 0, sizeof(a));
        for (char j: s) {
            a[j - 'a'] += 1;
        }
        int x = 0;
        for (int j = 0; j < 26; j++) {
            x = max(x, a[j]);
        }
        write(x > (s.size() >> 1) ? (x << 1) - s.size() : s.size() & 1);
        write('\n');
    }
}

破解谜题 (puzzle)

思路

暴力

考虑使用 DFS 处理每一次请求。直接从请求起始的位置开始往下搜索，直到满足题目给出的不再移动的条件停下，然后赋值即可。

DFS 函数如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
inline bool check(int x, int y) {
    if (x == r) {
        return true;
    }
    if (a[x + 1][y] == 'X') {
        return true;
    }
    if (a[x + 1][y] == 'O') {
        if ((a[x + 1][y - 1] != '.' || a[x][y - 1] != '.') && (a[x + 1][y + 1] != '.' || a[x][y + 1] != '.')) {
            return true;
        }
    }
    return false;
}

void dfs(int x, int y) {
    if (check(x, y)) {
        a[x][y] = 'O';
        return;
    }
    if (a[x + 1][y] == '.') {
        dfs(x + 1, y);
    } else if (a[x + 1][y] == 'O') {
        if (a[x + 1][y - 1] == '.' && a[x][y - 1] == '.') {
            dfs(x + 1, y - 1);
        } else {
            dfs(x + 1, y + 1);
        }
    }
}

用这种方法，可以获得 \(60 \rm pts\) 的好成绩。

正解

很显然，\(60 \rm pts\) 是无法使我们满意的，我们需要考虑如何优化。通过观察暴力做法，我们会发现，实际上对于同一列的路径，基本不会有太大的变化，只有末端会产生一点点的变动。因此我们可以考虑如何利用这种非常不错的性质。

考虑预处理每一列放置的路径，记录路径及其深度。每次放球的时候，从路径的最下方开始，判断路径是否仍合法，如果不合法，就回退，直到找到一个合法的点。从这个合法的点开始，更新路径、放球。这样就可以大幅度的优化程序的运行速度，成功 AC。

分析一下可得，这种方法的时间复杂度是 \(\mathcal{O}(nm^2) \leq 8 \times 10^8\) ，极限情况卡一卡能过，但是实际基本不可能跑满，故可以通过。

奇怪的思路

由于这一题是一道原题，所以可以找到一些牛鬼蛇神做法，就比如 lys 的分块做法。类似于正解，我们可以将路径分成若干段，然后每次更新已经错误的块。这种做法从复杂度上来说肯定是没有正解快的，但是仍然能正常通过原题。在这一题中，可能一些较小的块大小可以 AC，但是很遗憾 lys 的代码只能获得 \(60 \rm pts\) 的成绩。

代码

分块打法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
#include <bits/stdc++.h>

using namespace std;

template <typename T = int>
T read() {
    char c;
    while (c = getchar(), c < '0' || c > '9');
    T x = c ^ '0';
    while (c = getchar(), c >= '0' && c <= '9')
        x = x * 10 + (c ^ '0');
    return x;
}

const int N = 30000, M = 30, MS = M + 2, L = 50;
int n, m, bSum;
int bId[N + 2], bPos[N + 2], p[N + 2][MS];
char mp[N + 2][MS];

int get(int pos) {
    if (*(mp[0] + pos + MS) == '.')
        return *(p[0] + pos + MS);
    else if (*(mp[0] + pos + MS) == 'O') {
        if (*(mp[0] + pos - 1) == '.' && *(mp[0] + pos + MS - 1) == '.')
            return *(p[0] + pos + MS - 1);
        else if (*(mp[0] + pos + 1) == '.' && *(mp[0] + pos + MS + 1) == '.')
            return *(p[0] + pos + MS + 1);
    }
    return pos;
}

void build(const int i, const int xx) {
    const int le = bPos[i] + 1;
    if (xx == bPos[i + 1])
        for (int i = 1; i <= m; ++i)
            p[xx][i] = xx * MS + i;
    for (int i = xx - 1; i >= le; --i)
        for (int j = 1; j <= m; ++j)
            if (mp[i][j] == '.')
                p[i][j] = get(i * MS + j);
}
void bInit() {
    for (int i = 1; i <= n; ++i)
        bId[i] = (i - 1) / L;
    bSum = bId[n];
    for (int i = 0; i <= bSum; ++i)
        bPos[i] = i * L;
    bPos[bSum + 1] = n;
    for (int i = bSum; i >= 0; --i)
        build(i, bPos[i + 1]);
}

int main() {
    freopen("puzzle.in", "r", stdin);
    freopen("puzzle.out", "w", stdout);
    n = read(), m = read();
    for (int i = 1; i <= n; ++i)
        scanf("%s", mp[i] + 1);
    bInit();
    int q = read();
    while (q--) {
        int pos = *(p[0] + MS + read()), pp;
        while ((pp = get(pos)) != pos)
            pos = pp;
        mp[pos / MS][pos % MS] = 'O';
        build(bId[pos / MS], pos / MS);
    }
    for (int i = 1; i <= n; ++i)
        printf("%s\n", mp[i] + 1);
}

记忆化打法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
#include <iostream>

using namespace std;

char a[80009][109];
int r, c, n, x, path[109][80009], depth[109];

void dfs(int x, int y, int from) {
    path[from][x] = y;
    depth[from] = x;
    if (a[x + 1][y] != 'O' && a[x + 1][y] != '.') {
        return;
    }
    if (a[x + 1][y] == '.') {
        dfs(x + 1, y, from);
        return;
    }
    if (a[x + 1][y - 1] == '.' && a[x][y - 1] == '.') {
        dfs(x + 1, y - 1, from);
        return;
    }
    if (a[x + 1][y + 1] == '.' && a[x][y + 1] == '.') {
        dfs(x + 1, y + 1, from);
        return;
    }
}

void work(int x) {
    while (a[depth[x]][path[x][depth[x]]] != '.' && depth[x] > 0) {
        depth[x] -= 1;
    }
    dfs(depth[x], path[x][depth[x]], x);
    a[depth[x]][path[x][depth[x]]] = 'O';
}

signed main() {
    freopen("puzzle.in", "rt", stdin);
    freopen("puzzle.out", "wt", stdout);
    cin >> r >> c >> n;
    for (int i = 1; i <= r; i++) {
        for (int j = 1; j <= c; j++) {
            cin >> a[i][j];
        }
    }
    for (int i = 1; i <= c; i++) {
        dfs(1, i, i);
    }
    for (int i = 1; i <= n; i++) {
        cin >> x;
        work(x);
    }
    for (int i = 1; i <= r; i++) {
        for (int j = 1; j <= c; j++) {
            cout << a[i][j];
        }
        cout << endl;
    }
}

遥遥领先 (chase)

思路

看一眼题目，我们可以很容易的发现，这题似乎很像一道搜索题。没错，这题可以搜索，但是没法 AC。很容易发现，这个路线的答案会非常大，而搜索必须搜出每一种可能，这就会导致严重的时间超限。

但是良心的出题人为 DFS 准备了 \(20\) 分部分分，也为 BFS 的选手准备了 \(60\) 分部分分。

即使部分分很多，我们还是要考虑正解的写法。很显然，直接枚举是不可能的，因此我们可以考虑使用动态规划的方式统计路径的数量。为了方便，我们定义状态 \(f_{i,\, j,\, k,\, t}\) 为走到点 \((i,\,j)\)，转向 \(k\) 次，从 \(t\) 方向走来的路径数量（其中 \(t = 1\) 表示纵向、\(t = 2\) 表示横向）。设定完了状态，我们就需要考虑如何转移状态。很容易发现，我们需要分类讨论一下：

  • 不转向。此时 \(f_{i,\,j,\,k,\,1}=f_{i,\,j,\,k,\,1} + f_{i-1,\,j,\,k,\,1}\)，\(f_{i,\,j,\,k,\,2}=f_{i,\,j,\,k,\,2} + f_{i,\,j-1,\,k,\,1}\)。

  • 转向。在这种情况下，我们也是直接转移即可，但是要注意转向次数要 \(+1\)： \(f_{i,\,j,\,k,\,1} = f_{i,\,j,\,k,\,1}+f_{i,\,j - 1,\,k - 1,\,2}\)，\(f_{i,\,j,\,k,\,2} = f_{i,\,j,\,k,\,2} + f_{i - 1,\,j,\,k -1,\,1}\)。但是，对于最后一个状态，不应统计转向的情况。

需要注意的是初始值的安排：对于 \(f_{i,\,j,\,0,\,1}\)，在第一个纵向不能走的位置之前，这个状态的值为 \(1\)，此后为 \(0\)，横向的亦是如此。

至此，大事已成，简单实现即可。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
#include <iostream>
#include <cstring>

#define int long long
#define endl '\n'
#define mod 1000000007

using namespace std;

char a[250][250];
int t, n, m, f[250][250][250][3];

signed main() {
    freopen("chase.in", "rt", stdin);
    freopen("chase.out", "wt", stdout);
    cin >> n >> m >> t;
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            cin >> a[i][j];
        }
    }
    bool p1 = true, p2 = true;
    for (int i = 1; i <= n; i++) {
        p1 &= a[i][1] != '#';
        if (p1) {
            f[i][1][0][1] = 1;
        }
    }
    for (int i = 1; i <= m; i++) {
        p2 &= a[1][i] != '#';
        if (p2) {
            f[1][i][0][2] = 1;
        }
    }
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            if (a[i][j] == '#') {
                continue;
            }
            for (int k = 1; k <= t; k++) {
                f[i][j][k][1] += f[i - 1][j][k][1];
                f[i][j][k][2] += f[i][j - 1][k][2];
                f[i][j][k][1] %= mod;
                f[i][j][k][2] %= mod;
                if ((i != n || j != m)) {
                    f[i][j][k][1] += f[i][j - 1][k - 1][2];
                    f[i][j][k][2] += f[i - 1][j][k - 1][1];
                    f[i][j][k][1] %= mod;
                    f[i][j][k][2] %= mod;
                }
            }
        }
    }
    int ans = 0;
    for (int i = 0; i <= t; i++) {
        ans += f[n][m][i][1] + f[n][m][i][2];
        ans %= mod;
    }
    cout << ans;
}

积积积 (int)

前置知识

这道题作为附加题，还是十分优秀的。

我们可以看道题目中给出的式子： \[ \int^R_L f(x)\, \textrm{d}x \] 究竟是什么意思呢？其实就是求函数 \(f(x)\) 在 \(L\) 到 \(R\) 之间的定值积分。在讲求值之前，要先讲一下映射、函数和积分。

映射

再讲函数之前，先要讲一讲映射。首先我们考虑有两个非空集合 \(X\) 和 \(Y\)，如果存在一种法则 \(f\)，使得  \(X\) 中的每一个元素 \(x\)，按法则 \(f\)，在集合 \(Y\) 中有唯一确定的元素 \(y\)  与之对应。那么此时我们称 \(f\) 为 \(X\) 到 \(Y\) 的映射，形式化的记作： \[ f:X\to Y \]

在这之中，我们把  \(y\) 称为元素 \(x\) 在映射 \(f\) 下的像，记作：

\[ y=f(x) \]

而元素  \(x\) 称为元素 \(y\) 在映射 \(f\) 中的一个原像。

映射有两个必须知道的基本概念，值域和定义域。其中：

  • 值域：即映射的所有像组成的集合。

  • 定义域：即映射的所有原像组成的集合。

对于这道题，关于映射，这些就已经足够了，想了解更多，可以去翻看一下《高等数学第7版-上册》。

函数

或许接触过函数的人看到映射中那些名词会感觉有一些熟悉，这是应该的，因为从高等数学的角度上看，函数就是实数集（或它的子集）到实数集的一个映射。形式化的说：我们设数集 \(D\subset\mathbf{R}\)，则称映射 \(f:D\to \mathbf{R}\) 为定义在 \(D\) 上的函数，简记为： \[ y=f(x),\,x\in D \] 其中 \(x\) 称为自变量，\(y\) 为因变量，\(D\) 称为函数的定义域，记作 \(D_f\) 即 \(D_f=D\)。

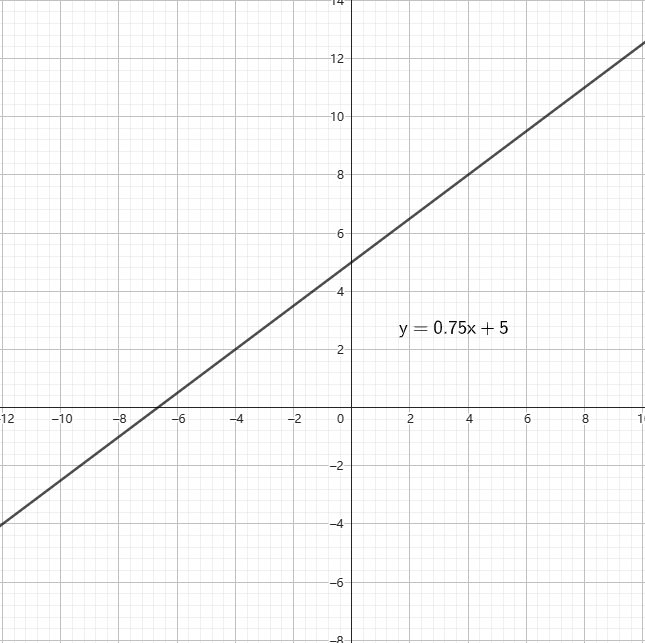
常见的函数有一次函数、二次函数、三角函数、对数函数等等，它们的函数图像如图。

图1-左：一次函数
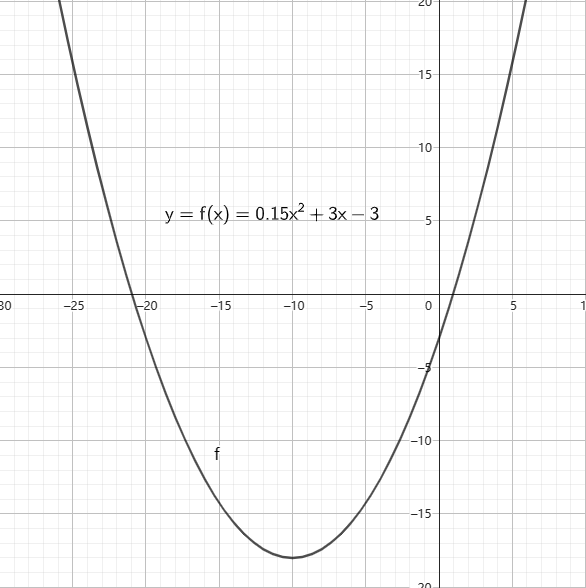
图1-右：二次函数
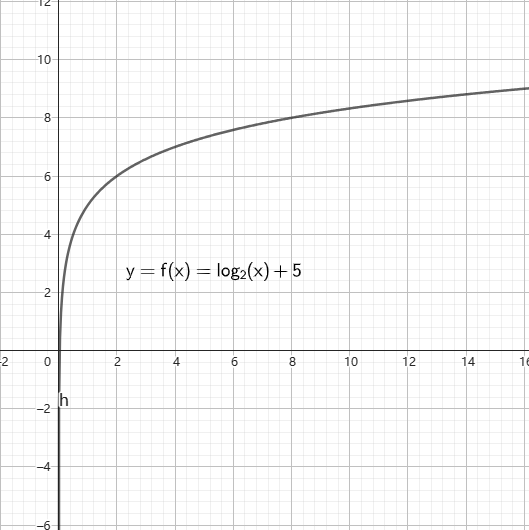
图2-左：对数函数
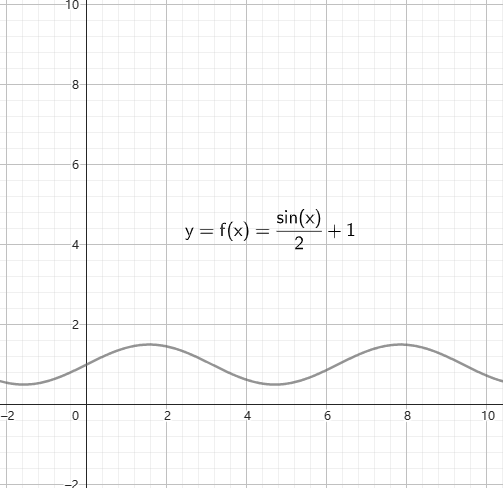
图2-右：三角函数

你还需要会知道一些函数的特性：

  • 函数的有界性：由于函数的定义域是一定的，这可能会导致函数的值域并不是整个实数域。

  • 函数的周期性：如果存在一个正数 \(l\)，使得 \(f(x)=f(x + l)\) 恒成立，那么我们称这个函数为周期函数，且我们称 \(l\) 是函数 \(f\) 的周期，一般地，我们称周期为函数的。正弦函数（\(\sin\)）就是常见的周期函数。

积分

积分问题通常被分为两类：不定积分和定积分。对于这道题，你只需要理解定积分。一般定积分以下属方式表达：

\[ \int_a^b f(x)\,\textrm{d}x \]

其中 \(b\) 为积分上限、\(a\) 为 积分下限，二者组成了一个积分区间 \([a,\,b]\)、\(f(x)\) 被称为被积函数，而 \(f(x)\,\textrm{d}x\) 称为被积表达式。

当然，聪明的你可定发现了，有些函数是不可以积分的，简称不可积。那么那些函数是可积的呢？《高等数学》告诉了我们答案：

  • 设 \(f(x)\) 在区间 \([a,\,b]\) 上连续，则 \(f(x)\) 在 \([a,\,b]\) 上可积。

  • 设 \(f(x)\) 在区间 \([a,\,b]\) 上有界，且只有有限个间断点，则 \(f(x)\) 在 \([a,\,b]\) 上可积。

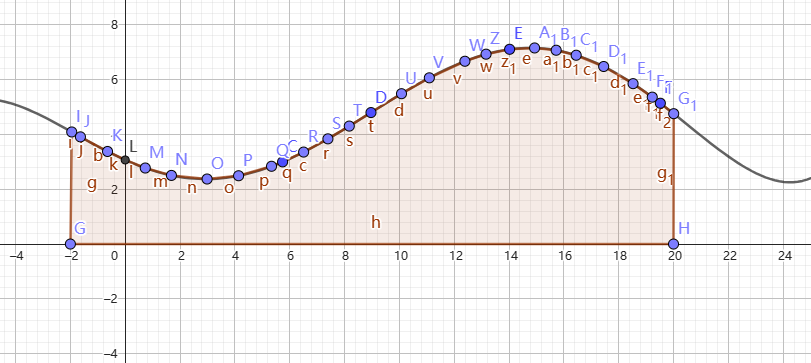
图3：定积分例1 - 普通函数

好的，那么积分是什么呢？实际上对于定积分，你可以认为他是在一段区间内函数值的和，但是这个求和是连续的，看到图3。图 3 中棕色的部分面积就是图中黑色函数在积分区间 \([-2,\,20]\) 的积分值。这就是积分的几何意义。

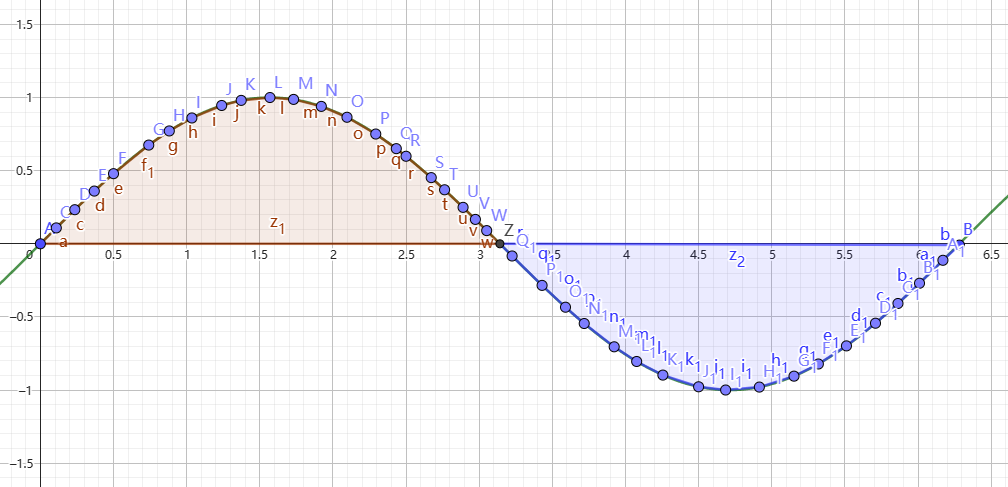
但是你可能会发现一个问题，就是如果函数在积分区间内有负值，那么怎么办呢？我么可以通过一个例子来理解这个问题。我们可以构造一个周期函数，然后尝试求他的积分值。图4就是一个正弦函数的图像。图像中棕色部分就是函数值为正的部分，区间为 \([0,\,\pi]\)，蓝色部分是函数值为负的部分，区间 \([\pi,\,2\pi]\) 我们可以大胆猜测一下，函数 \(\sin (x)\) 在区间 \([0, 2\pi]\) 的积分值是棕色部分减去蓝色部分，也就是 \(0\)。拿出计算器计算一下就会发现，结论正确。定积分值实际上就是函数位于\(x\) 轴上方部分的面积减去 \(x\) 轴下方的面积！

到这里，你已经基本掌握了做题所需的知识，让我们出发吧，旅行者！

图4：定积分例2 - 周期函数

思路

积分值计算

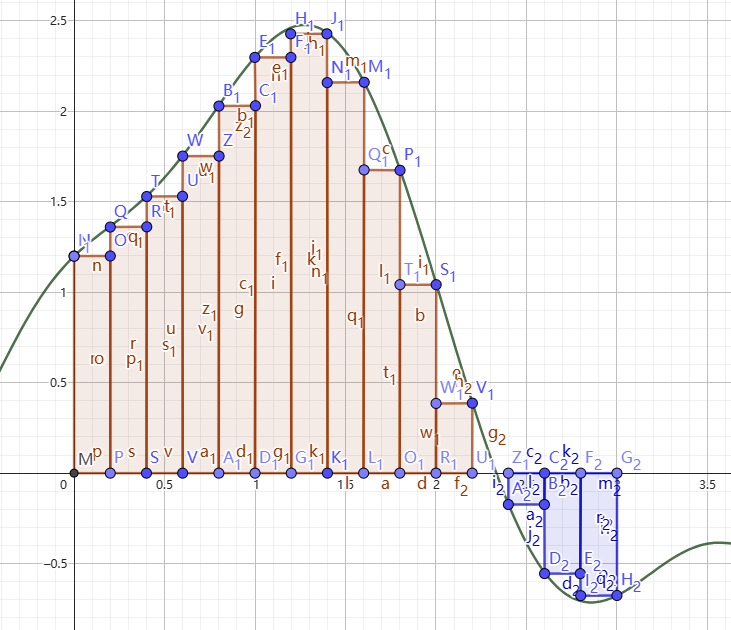
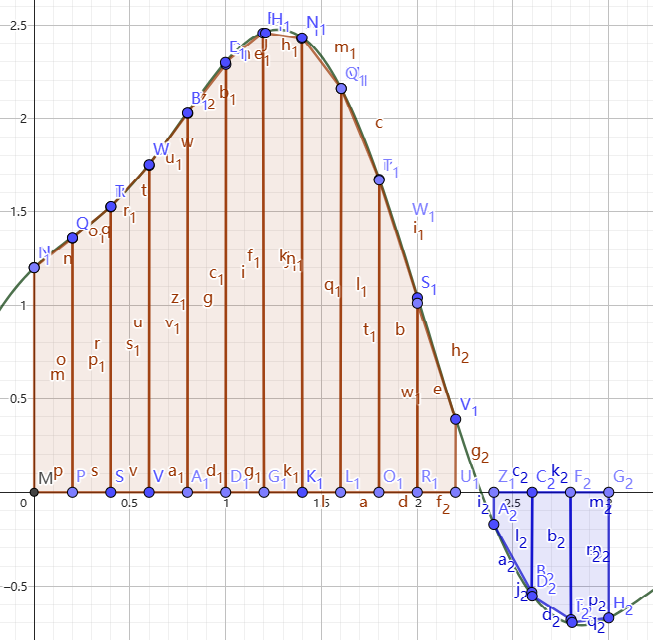
首先解决积分求值的问题，我们从最简单的矩形逼近开始。我们尝试把函数下的图形用矩形逼近，或者说常使用一些矩形把函数下的部分填满，如图5（左）。

图5-左：矩形逼近
图5-右：梯形逼近

很容易发现即使我们把面积分成这么多块，精度还是十分的低。我们考虑把矩形换成梯形，就像图 5（右）。这样看起来精度似乎提升了，但是效率似乎很低，我们亟需一种高效且精度高的定积分求值方式。

如果你翻看一篇内容杂糅的论文，你就会找到一种神奇的算法：辛普森法。这种算法使用一些二次函数来逼近我们要积的函数。

原论文中对算法数学推倒的过程非常少，因此下面给出一种 Simpson 公式的非原著推导过程，我们设 \(g(x) = ax^2+bx+c\) 为拟合后的函数，则推导过程如下：

\[ \begin{align*} \int_L^R f(x)\,\textrm{d}x &\approx \frac{1}{3}a\left(R^3-L^3\right)+\frac{1}{2}b\left(R^2-L^2\right)+c\left(R-L\right)\\ &= \frac{R-L}{6}\left(2a\left(L^2+LR+R^2\right)+3b\left(L+R\right)+6c\right)\\ &= \frac{R-L}{6}\left( aL^2+bL+c+aR^2+bR+c+4a\left(\frac{L+R}{2}\right)^2+4b\left(\frac{L+R}{2}\right) + 4c\right)\\ &= \frac{R-L}{6}\left(f(L)+4f\left(\frac{L+R}{2}\right)+f(R)\right) \end{align*} \]

这就是大名鼎鼎的辛普森公式：

\[ \int_L^R f(x)\,\textrm{d}x \approx \frac{R-L}{6}\left(f(L)+4f\left(\frac{L+R}{2}\right)+f(R)\right) \]

获得了辛普森公式，正当你计算时，你就会发现精度根本不足！因为一个二次函数很显然是不足以逼近一个复杂函数的。

为了解决精度问题，我们可以考虑将函数分段，我们可以将积分区间砍半，分为两次计算。每次都将区间砍半，直到精度达标。在估算精度的过程中，还存在着一个技巧。这个技巧在《数值分析》一书中有提到。

这个技巧来源于推广中值定理1。根据这个定理，我们可以发现当辛普森法算出来的积分值误差 \(\leq 15eps\) （\(eps\) 为给定的容差值（TOL）），那么这个值加上误差的 \(\frac{1}{15}\) 就是我们需要得到的足够精度的值了。具体证明参考原书 P240。

字符串解析

由于出题人非常毒瘤，给定的函数并不是固定的，他是由一个字符串表示的。这个字符串的格式是计算机难以识别的中缀表达式2。为了计算函数值，我们需要解析这个恶心的中缀表达式。

常见的解析中缀表达式的方式就是用栈来解析，具体过程如下：

  1. 转换为后缀表达式（逆波兰表达式）

    • 创建一个空栈和一个空输出列表。

    • 从左到右扫描中缀表达式：

    • 如果遇到操作数，添加到输出列表。

    • 如果遇到运算符，将其推入栈。

    • 如果遇到左括号，将其推入栈。

    • 如果遇到右括号，则弹出栈顶元素并添加到输出列表，直到遇到左括号。弹出左括号但不添加到输出列表。

    • 如果栈不为空，弹出所有剩余的运算符并添加到输出列表。

  2. 计算后缀表达式

    • 创建一个空栈。

    • 从左到右扫描后缀表达式：

    • 如果遇到操作数，将其推入栈。

    • 如果遇到运算符，弹出栈顶的两个操作数，进行计算，然后将结果推回栈。

    • 当后缀表达式被完全扫描后，栈顶的元素就是最终结果。

至此我们完成了题目的所有步骤，只需要将计算函数值和计算积分值两个部分结合一下即可。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
#include <bits/stdc++.h>

using namespace std;

typedef long double db;

int opl(char ch) {
    switch (ch) {
        case '+':
            return 1;
        case '-':
            return 1;
        case '*':
            return 2;
        case '/':
            return 2;
        case '^':
            return 3;
    }
    return -1;
}

int opv(char ch) {
    switch (ch) {
        case '+':
            return 1;
        case '-':
            return 2;
        case '*':
            return 3;
        case '/':
            return 4;
        case '^':
            return 5;
    }
    return -1;
}

int c = 0;
struct oper {
    int op, l, r;
} ope[114514];
db mem[114514];

int push(char op, int l, int r) {
    ope[++c] = oper{opv(op), l, r};
    return c;
}

int pre() {
    stack<int> v;
    stack<char> op;
    auto cc = [&]() {
        int a, b;
        b = v.top();
        v.pop();
        a = v.top();
        v.top() = push(op.top(), a, b);
        op.pop();
    };
    while (true) {
        if (cin.peek() == ')' || isspace(cin.peek())) {
            cin.get();
            while (!op.empty())cc();
            return v.top();
        } else if (cin.peek() == '(') {
            cin.get();
            v.push(pre());
        } else if (opl(cin.peek()) != -1) {
            char ch = cin.get();
            while (!op.empty() && opl(op.top()) >= opl(ch))cc();
            op.push(ch);
        } else if (isdigit(cin.peek())) {
            ++c;
            cin >> mem[c];
            v.push(c);
        } else if (cin.peek() == 'x') {
            cin.get();
            v.push(0);
        }
    }
}

db f(double x) {
    mem[0] = x;
    for (int i = 1; i <= c; ++i) {
        if (ope[i].op)
            switch (ope[i].op) {
                case 1:
                    mem[i] = mem[ope[i].l] + mem[ope[i].r];
                    break;
                case 2:
                    mem[i] = mem[ope[i].l] - mem[ope[i].r];
                    break;
                case 3:
                    mem[i] = mem[ope[i].l] * mem[ope[i].r];
                    break;
                case 4:
                    mem[i] = mem[ope[i].l] / mem[ope[i].r];
                    break;
                case 5:
                    mem[i] = pow(mem[ope[i].l], mem[ope[i].r]);
                    break;
            }
    }
    return mem[c];
}

db l, r;

db sps(db a, db b, db c, db l) {
    return l / 6.0 * (a + b + 4 * c);
}

const db eps = 1e-10;

db calc(db l, db r, db mid, db t, db fl, db fr, db fm) {
    db m1 = (l + mid) / 2.0, m2 = (mid + r) / 2.0;
    db fm1 = f(m1), fm2 = f(m2);
    db
            t1 = sps(fl, fm, fm1, mid - l),
            t2 = sps(fm, fr, fm2, r - mid);
    if (fabs(t1 + t2 - t) <= 15 * eps) return t1 + t2 + (t1 + t2 - t) / 15;
    return calc(l, mid, m1, t1, fl, fm, fm1) + calc(mid, r, m2, t2, fm, fr, fm2);
}

inline db g(db l, db r) {
    db mid = (l + r) / 2;
    db a = f(l), b = f(r), c = f(mid);
    return calc(l, r, mid, sps(a, b, c, r - l), a, b, c);
}

signed main() {
    freopen("int.in", "rt", stdin);
    freopen("int.out", "wt", stdout);
    cout << setprecision(6) << fixed;
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    pre();
    for (int i = 1; i <= c; ++i) {
        if (ope[i].op &&
            ope[i].l &&
            ope[i].r &&
            !ope[ope[i].l].op &&
            !ope[ope[i].r].op) {
            switch (ope[i].op) {
                case 1:
                    mem[i] = mem[ope[i].l] + mem[ope[i].r];
                    break;
                case 2:
                    mem[i] = mem[ope[i].l] - mem[ope[i].r];
                    break;
                case 3:
                    mem[i] = mem[ope[i].l] * mem[ope[i].r];
                    break;
                case 4:
                    mem[i] = mem[ope[i].l] / mem[ope[i].r];
                    break;
                case 5:
                    mem[i] = pow(mem[ope[i].l], mem[ope[i].r]);
                    break;
            }
            ope[i].op = 0;
        }
    }
    cin >> l >> r;
    cout << g(l, r);
}

致谢

首先我要向举办本场比赛的陈旭龙老师以及 TYOI 全体教练表示感谢，他们让我由于有了这次出题、讲题的机会。这次机会也为我本人带来了很大的水平提升。认识到做一个出题人有多么痛苦，背锅的压力有多么大。

其次要感谢在出题和学习过程中帮助过所有同学，包括但不限于带我入坑数学的曾奂霖、帮助写STD还在验题期间爆踩 STD 的苏昱霖、帮助我排除大坑的陈韦澔和沈歆迪......没有这些同学的帮助，这场如此优质的比赛一定不会诞生。

一定要感谢的是我的家人和学校为我带来了如此优质的学习环境，为我的 OI 生涯添砖加瓦。

最后感谢为本次比赛出题提供过帮助的所有人，包括但不限于 Lemon Lime 的开发者、Hydro 的开发者、VSCode 的开发者、GeoGebra的开发者、Desmos 的开发者、Mathworks 团队、Wolfram 团队、TexLive 以及 TexStudio 软件的开发者、《数值分析》的作者及译者、《高等数学》的作者、《算法导论》的作者及译者、CodeForces 运营团队、COCI 出题团队、辛普森本人，以及记不清的无数为出题提供过帮助的人。

  1. 见《数值分析》[@数值分析] P218↩︎

  2. 正常人类计算所用的算式↩︎

题解 > OiClass
#题解 #OiClass #公益赛
OiClass 2024 CSP-J 公益赛 #4 题解
https://lixuannan.github.io/posts/24397.html
作者
CodingCow Lee
发布于
2024年2月28日
许可协议