SPOJ MARTIAN 题解

思路

首先简单理解一下题目，会发现题目就是在网格上选择若干列（或列的上面一段）以及若干行（或行的左边一段）似的这些被选中的列和行之间的和最大。具体可以看题目的这张图：

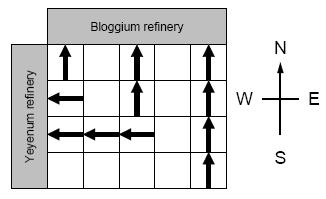
很明显这是一个 DP 问题，于是我们着手设计状态转移方程。首先我们先分别预处理出纵向的和横向的两个前缀和分别是 \(y_{i,\,j}\) 和 \(b_{i,\,j}\)，字母对应题目的矿物名称首字母。然后我们设状态 \(f_{i,\,j}\) 表示从这个位置开始到左上角的答案（最多的采矿数量和）。然后我们发现状态 \(f_{i,\,j}\) 只与 \(f_{i - 1, j}\) 和 \(f_{i,\, j - 1}\) 有关。

稍加思考即可得出我们的状态转移方程： \[ f_{i,\,j} = \max\left(f_{i - 1,\,j} + b_{i,\,j},\, f_{i,\,j - 1} + y_{i,\,j}\right) \] 于是就可以快乐 DP 了。

代码

#include <iostream>
#include <cstring>

using namespace std;

int n, m, y[509][509], b[509][509], f[509][509];

signed main() {
    while (cin >> n >> m) {
        if (n == 0 && m == 0) {
            return 0;
        }
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                cin >> b[i][j];
            }
        }
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                cin >> y[i][j];
            }
        }
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                b[i][j] += b[i][j - 1];
                y[i][j] += y[i - 1][j];
            }
        }
        memset(f, 0, sizeof f);
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                f[i][j] = max(f[i - 1][j] + b[i][j], f[i][j - 1] + y[i][j]);
            }
        }
        cout << f[n][m] << endl;
    }
}