这道题思路稍稍有那么一点绕

先理解一下题目，交叉着一点还是挺难理解的，我们把样例的图片画出来的话大概是这样的：

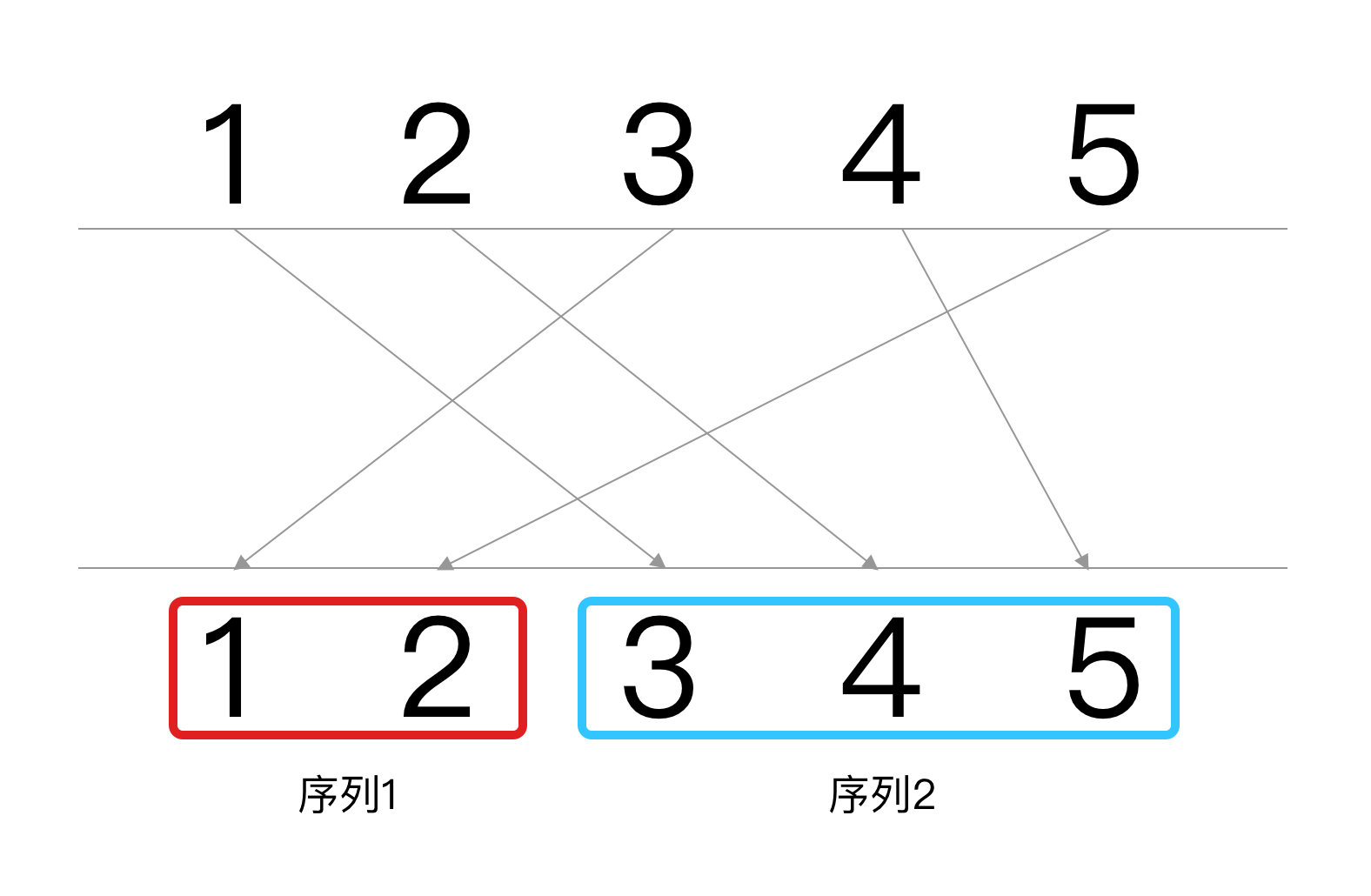
我们仔细观察一下，会发现，不交叉的的几项在下面（南岸）形成了一个上升序列（也可以说是不下降序列），那么求有多少项不交叉是不是可以改成当北岸按升序排好时南岸的数的最长不下降子序列的长度？这就很好理解了。先把北岸排序，让南岸跟着动，然后求南岸的最长不下降子序列的长度就可以得到答案了，下面就直接放代码了，最长不下降子序列（LIS）可以看这篇文章（也是我写的）

OK，直接看代码吧：

#include <iostream>
#include <algorithm>

using namespace std;

struct country {
    int n, s;
} a[5009];

bool cmp(country a, country b) {
    return a.n < b.n;
}

int n, x, y, ans, f[5009];

int main() {
    cin >> x >> y >> n;
    for (int i = 1; i <= n; i++) {
        cin >> a[i].n >> a[i].s;
        f[i] = 1;
    }
    sort(a + 1, a + n + 1, cmp);
    for (int i = 2; i <= n; i++) {
        for (int j = 1; j < i; j++) {
            if (a[j].s < a[i].s) {
                f[i] = max(f[i], f[j] + 1);
                ans = max(ans, f[i]);
            }
        }
    }
    cout << ans;
}