很明显,这道题是二分答案
那么,需要二分的是什么?有脑子都知道是,间距。那么求的究竟是最大值最小还是最小值最大呢?我们看到题目,我们需要求的是 “那么相邻两块土地之间的间隔的最大值” 也就是最小值最大。好的,那么框架有了,如下:
1 | |
那么 bool check(int x)
的函数题怎么写呢?额,我也不知道(doge)
\(\tiny 才怪。\) 开个玩笑。\(\Huge 进入正题\)。
题目要求我们寻找的这个数是两块土地之间的间隔的最大值,也就是说我们要在保证种满
\(m\)
块田的情况下让间距尽量远,我们用二分的方法枚举田之间的距离,然后判断距离是否可行,如果可行,就尝试更大的值,如果不行,就尝试更小的值,直到形成半封闭区间:\(r - l ≤ 1\) 时, \(l\) 的值即为所求,注意,输入的数组 \(a\)
是无序的,需要先排序(sort(a + 1, a + n + 1))
对于函数 bool check(int x) 我们希望他能够判断在距离为
\(x\) 的情况下是否有 \(≥ m\) 的田被耕种,如果是,返回 \(true\) 否则为 \(false\)
。为了达到这个功能,我们需要从第一块田开始,枚举间距大于 \(n\) 的所有田,将数量计入变量 \(cnt\) 最后会有两种可能 \[
\left\{
\begin{array}{lr}
cnt\ge m,\ return\ true; \newline
cnt < m, \ return\ false;
\end{array}
\right.
\] 非常简单 \(\Huge 才怪\)
当我兴致勃勃的把代码打出来的时候,我翻车了,代码如下:
1 | |
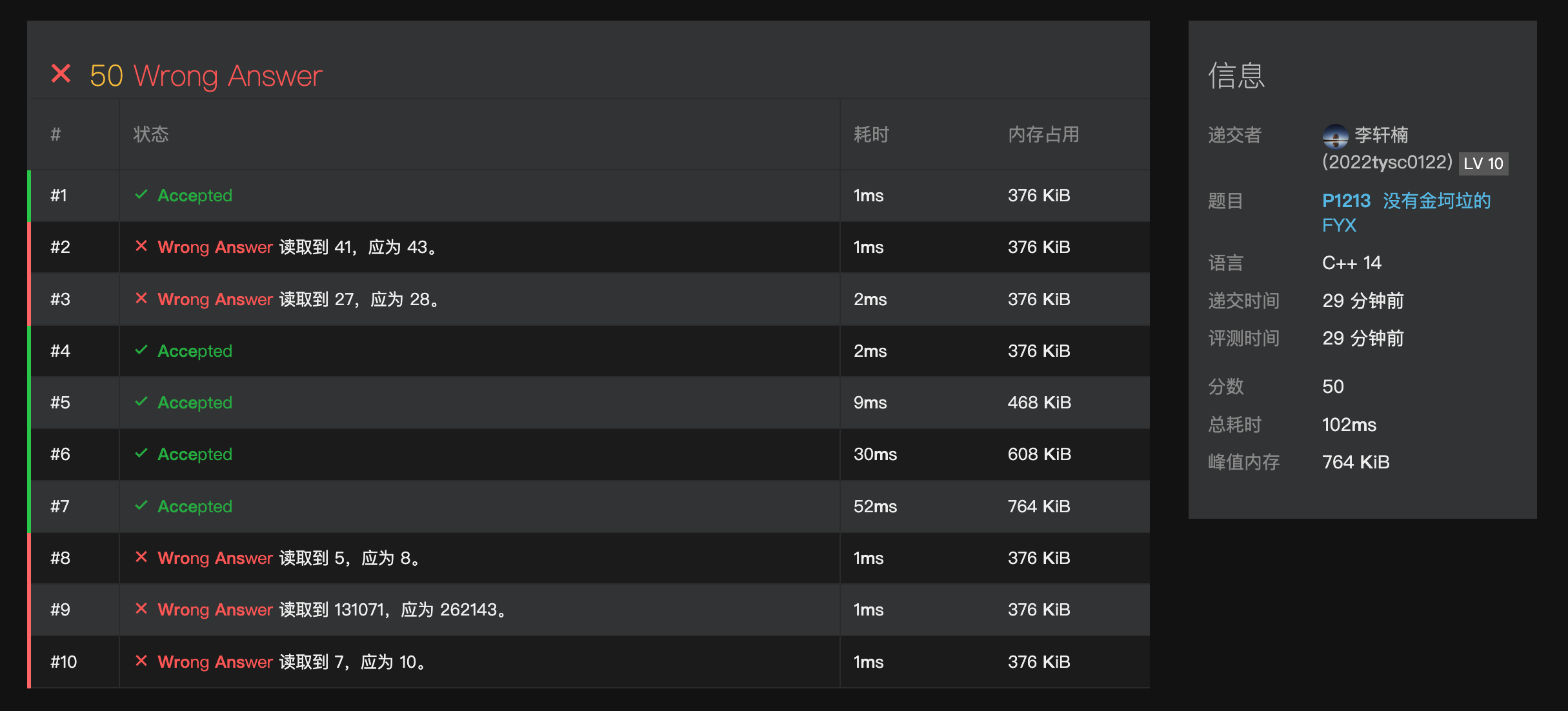
非常成功的失败了,但是我久久找不出原因
两个星期后已经是新的一年了(2023),我终于找到了错误的原因。简单重写了一下代码,如下:
1 | |
没有采用 lower_bound() 直接算 \(i\) 的方法,而是以 \(O(n)\)
的时间复杂度便利数组,激动的心,颤抖的手,我点了编译运行,复制样例,粘贴,\(\Huge 输出\ 1\ ?\) 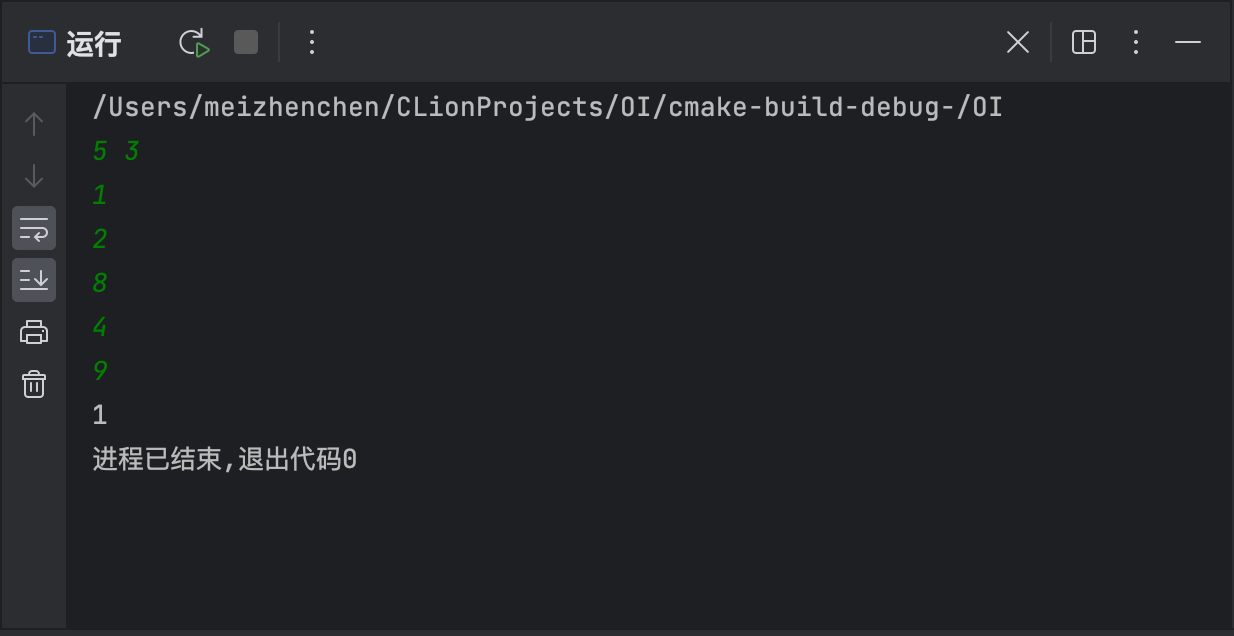 我当场差点 \(\Tiny 去世\) 好吧,让我康康有什么
BUG。原来如此。我真的是个 \(\Huge
大聪明\) 我居然忘记把 \(a[i]\)
给算进种过的田里面,也就是说,我的 \(cnt\) 一直是比正常的 \(cnt\) 小一的(\(cnt_{我的} + 1=cnt_{正常的}\)) 那么就让我把
\(cnt\) 的初始值设置为 \(1\) 吧,编译运行,果然成功
我当场差点 \(\Tiny 去世\) 好吧,让我康康有什么
BUG。原来如此。我真的是个 \(\Huge
大聪明\) 我居然忘记把 \(a[i]\)
给算进种过的田里面,也就是说,我的 \(cnt\) 一直是比正常的 \(cnt\) 小一的(\(cnt_{我的} + 1=cnt_{正常的}\)) 那么就让我把
\(cnt\) 的初始值设置为 \(1\) 吧,编译运行,果然成功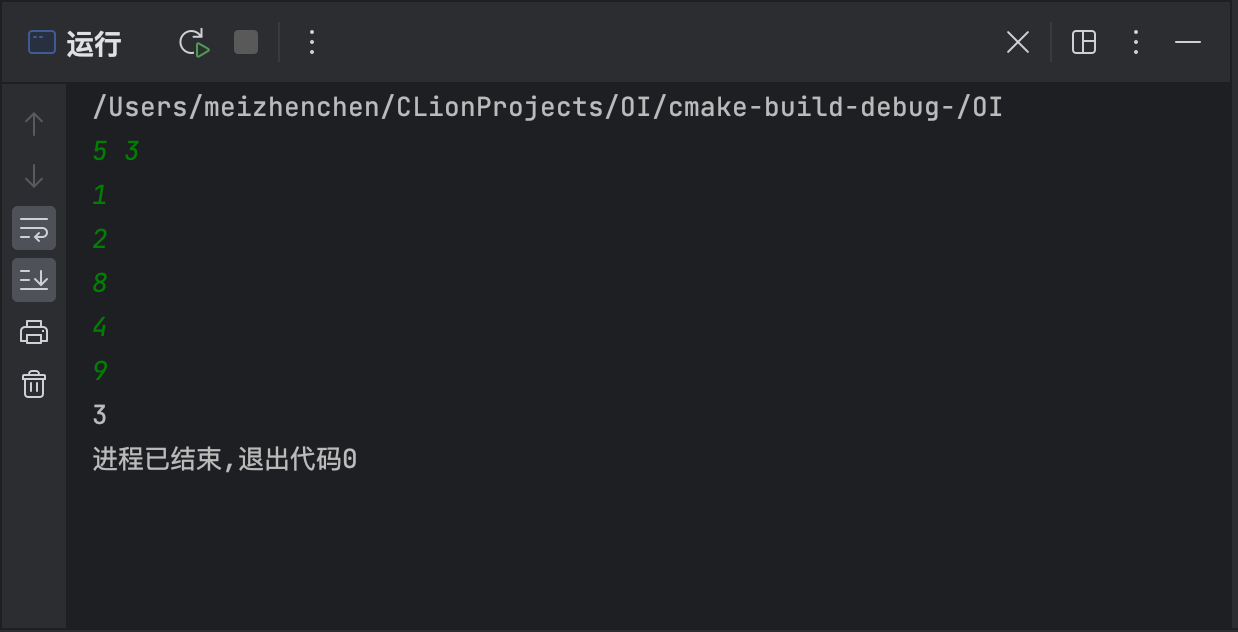
OK,那么下面就是激动人心的提交时刻,复制粘贴提交\(\Huge AC\ !!!!\)
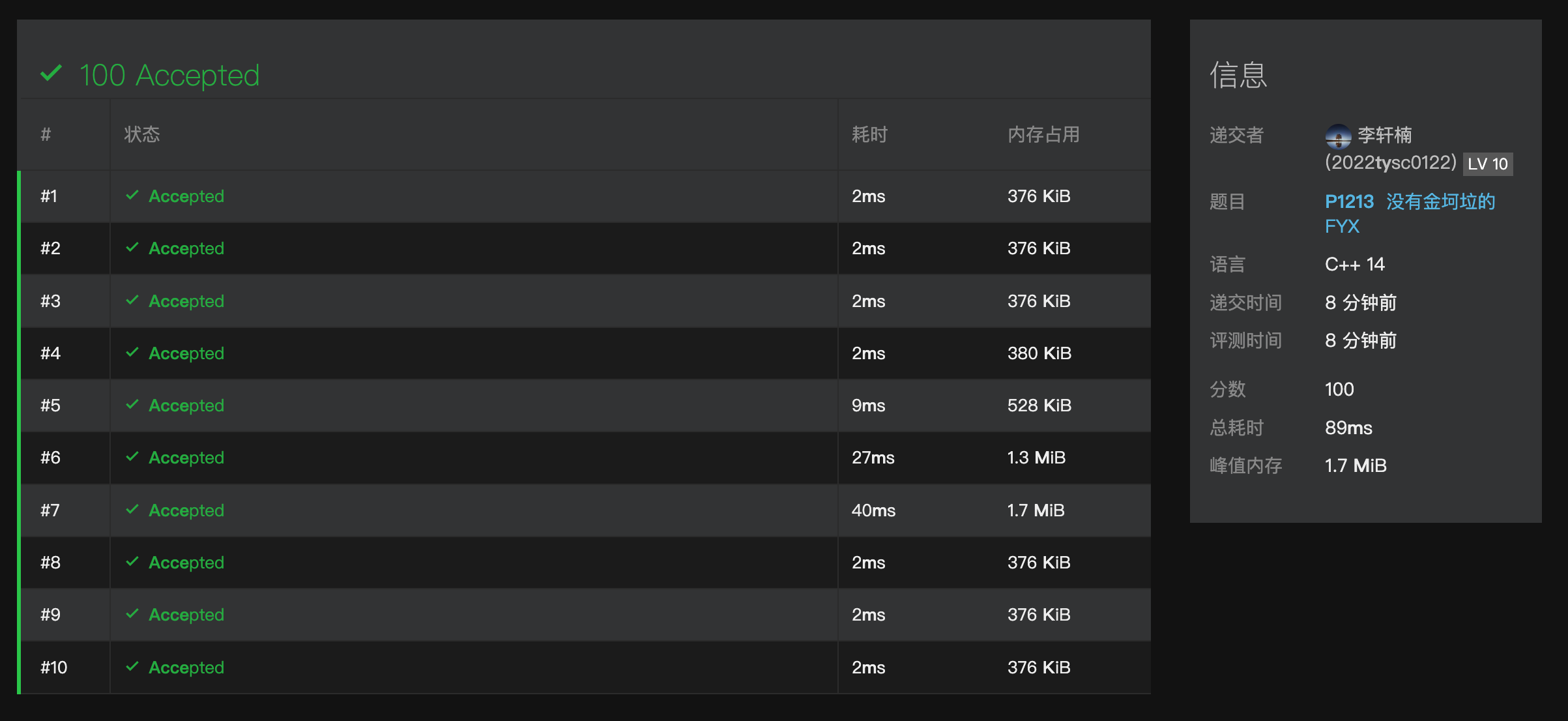
终于完成了。
“觉得不错的话,给点打赏吧 (✿◕‿◕✿)”

微信支付

支付宝支付 (暂不支持)